要么改变世界，要么适应世界

逻辑回归-手写字符识别

2022-04-25 12:31:07
0
机器学习
目录

前言

逻辑回归虽然在名字里边带了逻辑，但是经常被用于分类问题，而且常和线性回归相结合，本文将利用MNIST数据集，完成多分类问题，带你一窥逻辑回归背后的原理。

相关原理

数据集获取

下载地址

该数据集中包含了6万个训练集样本、1万个测试集样本，每个样本都是28*28的字符图片，标签为该字符对应的字符类别，下图为某一个样本：

获取数据集以后，我们还要将图片降维，使之变为长度784的向量，意味着我们有784个特征，虽然提取特征有更好的方法，但是我们这里仍然使用线性回归的方法。

此外，每份样本的标签值是该样本的类别，还应该进行独热编码，将其转为每个类别的概率。

sigmoid函数

该函数也称为逻辑函数，函数定义如下：

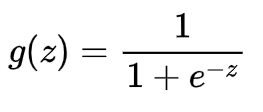
g(z)=\frac{1}{1+e^{-z}}

函数大概长这样：

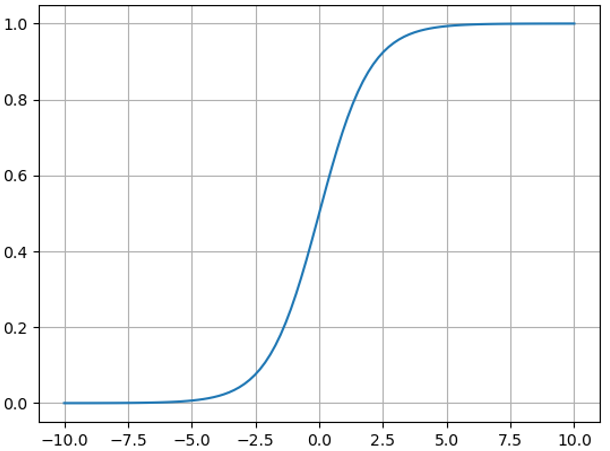
g(z)=\frac{1}{1+e^{-z}}

它很符合我们的直观感觉，在无穷大或者无穷小的时候，变化不大，要么趋于1要么趋于0，而在中间位置变化最为明显，我们也可以求得其导数：

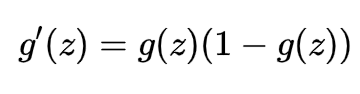
g'(z)=g(z)(1-g(z))

Forward propagation（前向传播 ）

该过程是从输入到输出的过程，即从图片输入到计算其每一个类别概率的过程，如果是二分类问题，那么输出则是该图片属于该类别的概率，若是多分类，那么输出的个数应该与类别数量一致，其每一个输出对应类别的概率。

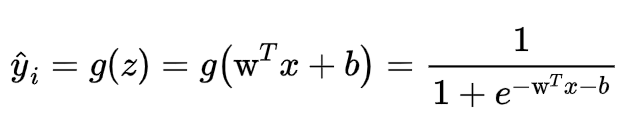
\widehat{y}_{i}=g(z)=g\left(\mathrm{w}^{T} x+b\right)=\frac{1}{1+e^{-\mathrm{w}^{T} x-b}}

这里的 w就是我们图片每一个像素对应的权重，故长度也为784

Back propagation （反向传播）

反向传播指的是从根据输出，计算梯度，更新参数的过程，这里使用的仍然是梯度下降分析法。不过我们先介绍一下交叉熵的概念，这个一般用于衡量两个概率分布的距离，也可以说用来判断两个模型之间有多“像”，该函数定义如下：

我们也是用该函数作为我们的损失函数。

该函数对z求导为：

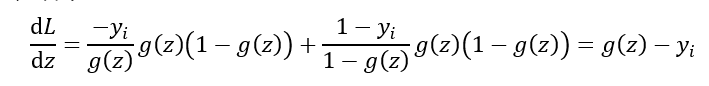
\frac{\mathrm{d}L}{\mathrm{d}z}=\frac{-y_i}{g\left(z\right)}g\left(z\right)\left(1-g\left(z\right)\right)+\frac{1-y_i}{1-g\left(z\right)}g\left(z\right)\left(1-g\left(z\right)\right)=g\left(z\right)-y_i

进一步地，对参数w求导

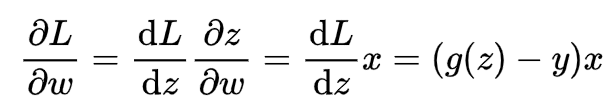
\frac{\partial L}{\partial w}=\frac{\mathrm{d} L}{\mathrm{d}z}\frac{\partial z}{\partial w}=\frac{\mathrm{d} L}{\mathrm{d}z}x=\left(g\left(z\right)-y\right)x

同理，对b求导

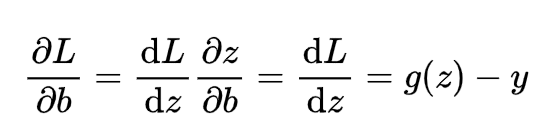
\frac{\partial L}{\partial b}=\frac{\mathrm{d} L}{\mathrm{d}z}\frac{\partial z}{\partial b}=\frac{\mathrm{d} L}{\mathrm{d}z}=g\left(z\right)-y

softmax 函数

由于我们的输出有多个，具体来说，输出个数k等于类别数，本数据集而言，有10个，这样就势必带来一个问题，所有的概率加起来和可能不为1，这显然违背常理，因此要进一步处理输出，我们使用softmax函数，该函数定义如下：

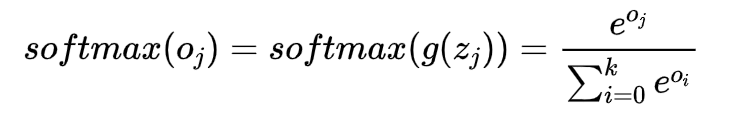
softmax\left(o_j\right)=softmax\left(g\left(z_j\right)\right)=\frac{e^{o_j}}{\sum_{i=0}^{k}e^{o_i}}

训练代码

import numpy as np
import matplotlib.pyplot as plt
import gzip
import pickle

class LogicTrain:

    def start_tain(self, epoch, learning_rate):
        
        fig = plt.figure()
        cost_ax = fig.add_subplot(1, 2, 1)
        cost_ax.set_title("Loss change process")
        accuracy_ax = fig.add_subplot(1, 2, 2)
        accuracy_ax.set_title("accuracy")

        training_inputs, training_labels, validation_inputs, validation_labels, test_inputs, test_labels = self.load_binary_data()
        # feature_num 是 784，即每一张图片拉成一维的向量的长度
        n, feature_num = training_inputs.shape
        k = 10

        accuracy_x, accuracy_y = [], []
        w, b = self.init_parameter(feature_num, k)

        cost_x, cost_y = [], []
        for i in range(epoch):
            y_hat = self.forward(training_inputs, w, b)
            w, b = self.backward(training_inputs, w, b, training_labels, y_hat, learning_rate)
            crs_etr = self.cross_entropy(training_labels, y_hat)
            loss = np.sum(crs_etr) / n / k
            print(' epoch = ', i, ' loss = ', loss)
            cost_x.append(i)
            cost_y.append(loss)
        # 计算预测验证集的准确性
        vl_hat = self.forward(validation_inputs, w, b)
        vl_predict = self.softmax(vl_hat)
        # 找出概率最大的下标，即最可能的字符
        predict_label = np.argmax(vl_predict, axis=1)
        predict_right_number = np.sum((predict_label == validation_labels).astype(np.int))
        m = validation_labels.shape[0]
        accuracy = predict_right_number / m
        print('The accuracy rate is:', accuracy)
        cost_ax.plot(cost_x, cost_y)
        accuracy_x.append('lr=' + str(learning_rate) + '&epoch=' + str(epoch))
        accuracy_y.append(accuracy)
        
        self.save_model(w, b)
        accuracy_ax.bar(accuracy_x, accuracy_y)
        plt.show()

    def load_binary_data(self):
        # 该数据集已经将图片转为行向量  即每一张图片都被拉成一维向量了
        f = gzip.open('mnist.pkl.gz', 'rb')
        training_data, validation_data, test_data = pickle.load(f, encoding='bytes')
        f.close()

        training_inputs, training_labels = training_data
        validation_inputs, validation_labels = validation_data
        test_inputs, test_labels = test_data

        # 实际上字符识别，模型可能更关心该点像素是不是属于字符中的一部分
        # 因此可以将像素二值化，将灰度值信息去掉，直接 0 或者 1
        training_inputs[training_inputs < 0.01] = 0
        training_inputs[training_inputs >= 0.01] = 1

        validation_inputs[validation_inputs < 0.01] = 0
        validation_inputs[validation_inputs >= 0.01] = 1

        test_inputs[test_inputs < 0.01] = 0
        test_inputs[test_inputs >= 0.01] = 1

        # 10 分类问题
        k = 10

        training_labels = self.one_hot_encoding(k, training_labels)

        return (training_inputs, training_labels, validation_inputs, validation_labels, test_inputs, test_labels)

    def one_hot_encoding(self, k, original_label):
        label = np.eye(k)[original_label].reshape(-1, k)
        return label

    def init_parameter(self, n, k):
        w, b = np.random.randn(n, k), np.random.randn(1, k)
        return w, b

    def forward(self, x, w, b):
        z = np.dot(x, w) + b
        return self.sigmoid(z)

    def sigmoid(self, X):
        return 1.0 / (1.0 + np.exp(-X))

    def backward(self, x, w, b, y, y_hat, l_rate):
        m = x.shape[0]
        dw = 1.0 / m * np.dot(x.T, y_hat - y)
        db = 1.0 / m * np.sum(y_hat - y)
        w = w - l_rate * dw
        b = b - l_rate * db
        return w, b

    def cross_entropy(self, y, y_hat):
        return -(y * np.log(y_hat + 1e-10) + (1 - y) * np.log(1 - y_hat + 1e-10))

    def softmax(self, x):
        x_exp = np.exp(x)
        partition = np.sum(x_exp, axis=1).reshape(-1, 1)
        return x_exp / partition
    def save_model(self, w, b):
        model = np.vstack((w, b))
        np.save('params-binarization.npy', model)
        
if __name__ == "__main__":
    l = LogicTrain()
    l.start_tain(500, 0.5)

训练结果：

应用模型

训练结束以后，我们将学习得到的参数w和b保存，接下来我们就可以测试我们模型的性能了，使用之前先将参数导入，然后再使用，这里借助OpenCV和PyQt，主要是获取鼠标的轨迹，然后转为图片，并放到我们的模型中计算每一个类别的概率，再选择最大的作为输出即可。

import numpy as np
import matplotlib.pyplot as plt
import gzip
import pickle
import cv2
from PyQt5.QtWidgets import QMessageBox

class LogicApplication:
    def start(self):
        # 初始化全局参数
        self.drawing = False
        self.ix, self.iy = -1, -1
        self.image = np.zeros((512, 512, 3), np.uint8)

        window = cv2.namedWindow('write your number')
        cv2.setMouseCallback('write your number', self.draw_circle)

        # 大小是 785 * 10
        param = self.load_model()

        w, b = param[0:784, :], param[-1, :]

        ENTER, SPACE, ESC = 13, 32, 27
        while (1):
            cv2.imshow('write your number', self.image)
            k = cv2.waitKey(50) & 0xFF
            # 按下 enter 键，识别当前画布上的数字
            if k == ENTER:
                print('enter')

                img_new = cv2.cvtColor(self.image, cv2.COLOR_BGR2GRAY)
                cv2.imwrite("write.jpg", self.image)
                x = self.handle_img(self.image)
                predict_y = self.softmax(np.dot(x.reshape(1, -1), w) + b)
                # 找出概率最大的下标，即最可能的字符
                predict_label = np.argmax(predict_y, axis=1)

                self.show_message(predict_label, predict_y)

                print('you wirte : ', predict_label)
                print('Each probability is '.join(str(i) for i in np.round(predict_y, 2)))
            # 按下 space 键，清空当前图像，还原成黑色画布
            elif k == SPACE:
                self.image = np.zeros((512, 512, 3), np.uint8)  # 清空
            # 按下 “ESC” 键，退出程序
            elif k == ESC:
                break
        cv2.destroyWindow('write your number')
    def load_model(self):
        param = np.load('params-binarization.npy')
        return param

    def handle_img(self, img):
        # 将图像等比例缩小至28x28大小
        img = cv2.resize(img, (28, 28))
        # 转化为灰度图
        im_arr = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
        # 把图像矩阵转化为一维向量
        x = im_arr.reshape(-1, 1)

        x[x < 128] = 0
        x[x >= 128] = 1
        return x

    # 鼠标手写数字
    def draw_circle(self, event, x, y, s, a):
        if event == cv2.EVENT_LBUTTONDOWN:
            self.drawing = True
            self.ix, self.iy = x, y
        elif event == cv2.EVENT_MOUSEMOVE:
            if self.drawing == True:
                # 圆半径（笔画粗细）设置为25是为了和mnist数据集中的数字尽可能粗细相似
                cv2.circle(self.image, (x, y), 25, (255, 255, 255), -1)  # 画笔颜色为白色
        elif event == cv2.EVENT_LBUTTONUP:
            self.drawing = False
            cv2.circle(self.image, (x, y), 25, (255, 255, 255), -1)

    def softmax(self, x):
        x_exp = np.exp(x)
        partition = np.sum(x_exp, axis=1).reshape(-1, 1)
        return x_exp / partition

    def show_message(self, predict_label, predict_y):
        message_body = "预测您输入的字符为：" + str(predict_label) + "，其中，各个字符的预测概率为：\n"
        for index, probability in enumerate(predict_y[0]):
            message_body += str(index) + "："+str(round(probability, 3)) + "，"
        message_body += "\n结果仅供参考"

        messageBox = QMessageBox()
        messageBox.setWindowTitle('预测结果')
        messageBox.setText(message_body)
        messageBox.setStandardButtons(QMessageBox.Yes | QMessageBox.No)
        buttonY = messageBox.button(QMessageBox.Yes)
        buttonY.setText('好的（并清空笔记）')
        buttonN = messageBox.button(QMessageBox.No)
        buttonN.setText('好的')
        messageBox.setStyleSheet("QPushButton:hover{background-color: rgb(255, 93, 52);} QLabel{font: 14pt \"微软雅黑\"; min-width: 900px;}")
        messageBox.exec_()
        if messageBox.clickedButton() == buttonY:
            self.image = np.zeros((512, 512, 3), np.uint8)  # 清空
        
if __name__ == "__main__":
    # l = LogicTrain()
    # l.start_tain(500, 0.5)
    a = LogicApplication()
    a.start()

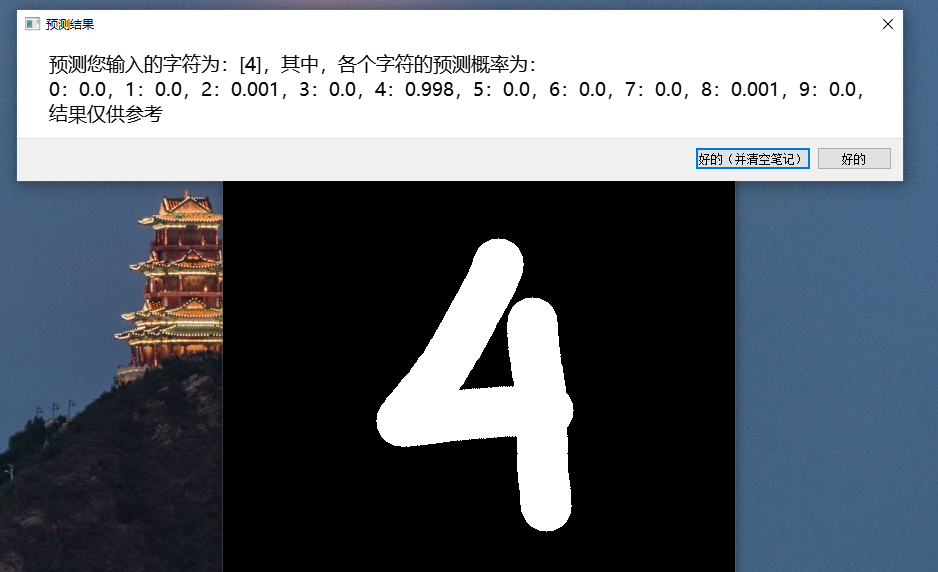
效果如图

逻辑回归 MNIST

本文由「黄阿信」创作，创作不易，请多支持。

如果您觉得本文写得不错，那就点一下「赞赏」请我喝杯咖啡~

商业转载请联系作者获得授权，非商业转载请附上原文出处及本链接。

关注公众号，获取最新动态！

历史评论
开始评论
正在加载今日诗词....
本站已在此等您 1350 日 04 时 12 分 06 秒
2020 - 2024 by Yalexin
桂ICP备20003049号-1