numpy实现线性回归模型

前言

生活中常常遇到线性模型的例子，例如房子的价格与占地面积几乎是呈线性，它还可能和卧室数量相关；又如一个学生是否具备获取奖学金资格与学生成绩、参与竞赛经历、班干部任职经历都相关；又如一个大学生是否能够在大学中脱单，与个人相貌、为人处事能力、生活习惯都有联系。

相关原理

以预测房子价格为例，如果将房子面积x1、卧室数量x2作为特征，房子价格为目标，则可以表示为：

式子中的w代表相应的特征权重，b代表偏置。

用向量可以表示为：

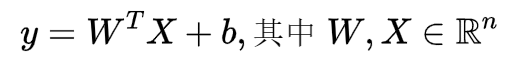
而我们的目标是对于给定数据集，我们求出最符合的参数w1和w2，以及b，使得模型很好地贴近数据集，我们该如何度量我们的模型是否和数据集贴近呢？我们这里平方差来表示二者的差距，计算该平方差的函数我们称之为损失函数，我们的样本的预测值为y_hat，真实值为y，则损失函数如下：

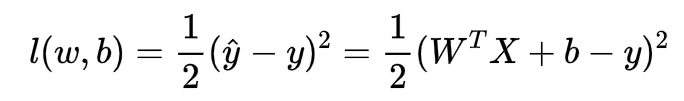
上面的常数1/2并不是硬性要求，只是为了方便后面求导使得系数变为1。

因此问题转变成找到一组参数，使得所有样本的损失和变得最小，即

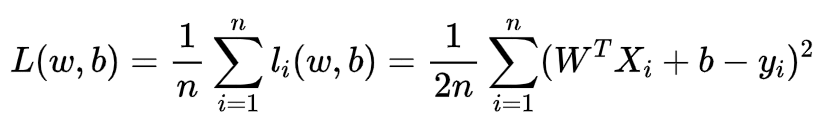
实际上也是在求上述函数的极小值。为了方便运算，我们可以将参数w和b合并，并在x右边增加一列：

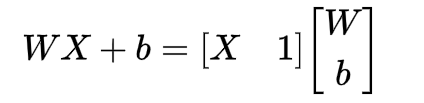
即损失函数又可以表示为：

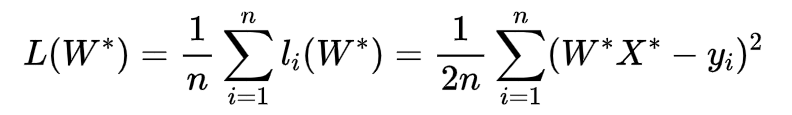
小学二年级的数学老师告诉我们，这个是关于自变量W*（注意，这里的x和y都是常量）的二次函数，有极值，那我们该怎么求解？数学老师继续告诉我们，二次函数极值可以利用公式！当然也可以使用梯度下降分析法，因为有些模型不可以用公式直接求解极值！

梯度下降分析法参数更新方式是：w = w - learning_rate * grad，grad是在该点的梯度，即导数（可以粗略地称为导数，但是严格来说这样子的说法是错误的）

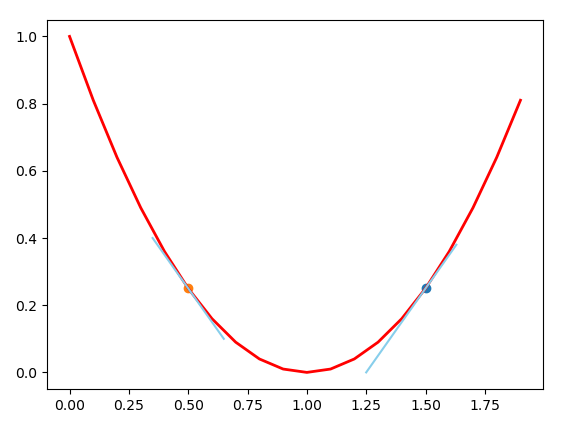
如上图所示，对于左边的点，其导数为负数，减去一个负数（learning_rate 我们称之为学习率，是正数）后其值增大，即经过更新后，自变量w往右边走了一段距离，对于右边的，更新后自变量往左边走了一段距离，最终我们的w将趋于1.0，即极值点附近。

损失函数对W求导为：

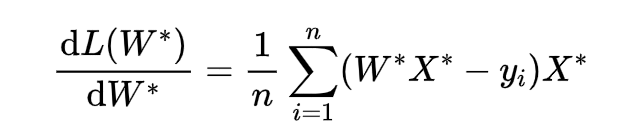
回归实现

简单起见，我们假设只有一个特征，即只有一个x，而不是有x1,x2,...我们首先生成一组线性数据，为了更符合实际，我们加入随机偏差：

def data():
    x = np.linspace(-20, 20, 50)
    y = 2*x + 3 + np.random.randn(len(x)) * 3
    x = x.reshape(-1, 1)
    y = y.reshape(-1, 1)
    return x, y

然后初始化我们的参数w,b

def init():
    w, b = np.random.randn(), np.random.randn()
    # 参数合并
    return np.array([[w],
                     [b]])

定义误差函数

def l(W, X, y):
    WX = np.dot(X, W) - y
    return WX ** 2 / 2.0

定义损失函数：

def loss(W, X, y):
    l_value = l(W, X, y)
    n = X.shape[0]
    return np.sum(l_value) / n

梯度下降法：

def gradient_descent(W, X, y):
    n = y.shape[0]
    A = np.dot(X, W) - y
    return np.dot(X.T, A) / n

开始我们的训练：

def train():
    learning_rate, epoch = 0.01, 100
    W = init()
    x, y = data()
    one = np.ones((x.shape[0],1))
    X = np.c_[x, one]
    loss_x, loss_y = np.zeros((epoch, 1)), np.zeros((epoch, 1))
    for i in range(epoch):
        loss_value = loss(W, X, y)
        print("epoch = ", i, "loss = ", loss_value)
        loss_x[i] = i
        loss_y[i] = loss_value
        
        grad = gradient_descent(W, X, y)
        W = W - learning_rate * grad
    plt.subplot(1, 2, 1)
    plt.scatter(x, y)
    plt.plot(X[:, 0], np.dot(X, W), color='red')
    
    plt.subplot(1, 2, 2)
    plt.title("loss")
    plt.plot(loss_x, loss_y)

结果

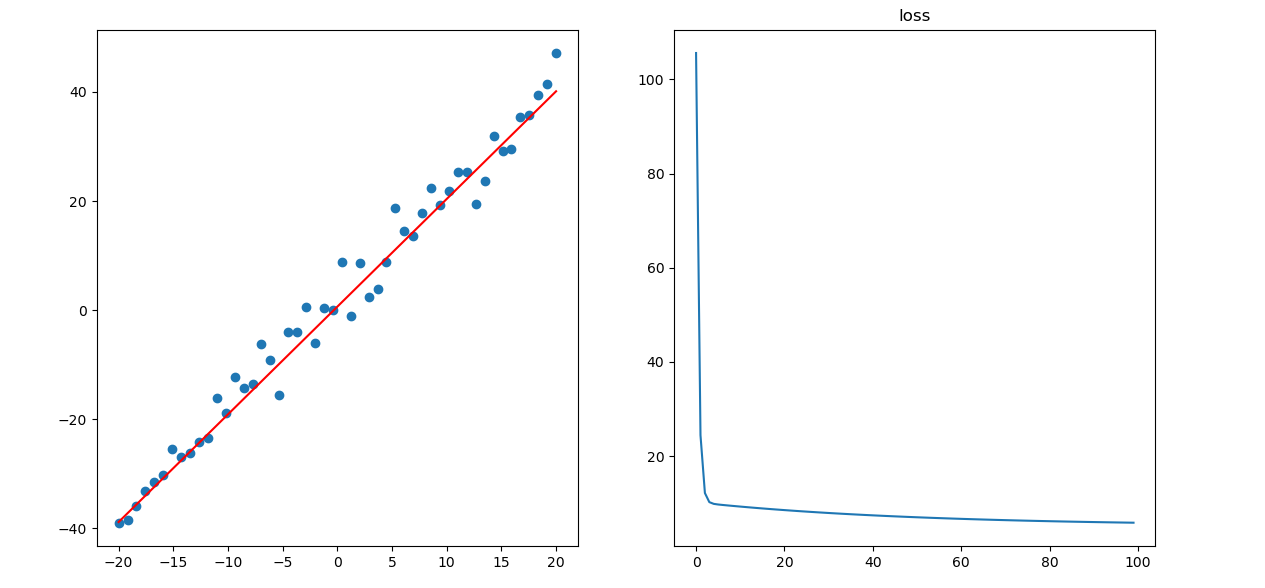
可以发现，拟合效果还是挺不错的，损失值下降得也挺快，前面的急剧下降是因为我们是随机初始化的参数，该参数对应的导数可能比较大，因此更新得比较快。前面的急剧下降是因为我们是随机初始化的参数，该参数对应的导数可能比较大，因此更新得比较快。