手撕红黑树！使用C语言带你实现一个平衡搜索树【正文】

认识红黑树

上篇文章我们主要认识了二叉树搜索树，这篇文章正式介绍红黑树。

红黑树在二叉搜索树的基础上，加了些性质，包含color、key、left、right、p，颜色取值为红色或者黑色，此外，我们把NIL节点视为特殊的节点，具体而言，视为外部节点，也叫叶子节点，把带有关键字的节点视为内部节点。

红黑树是具有下面性质的二叉搜索树：

1. 每个节点，要么是红色的，要么是黑色的。
2. 根节点是黑色的。
3. 每个叶子节点（NIL）是黑色的。
4. 如果一个节点是红色的，那么它的两个子节点都是黑色的（如果子节点是NIL，则子节点也是黑色的）
5. 对于每个节点，从该节点到其所有后代叶节点的简单路径（即只会从该节点往叶子节点向往下）上，均包含相同数目的黑色节点。

我们把bh(x)定义为从节点x开始（不包括该节点）到叶子节点的任意一条简单路径上的黑色节点个数成为黑高（black-height）。

例如：

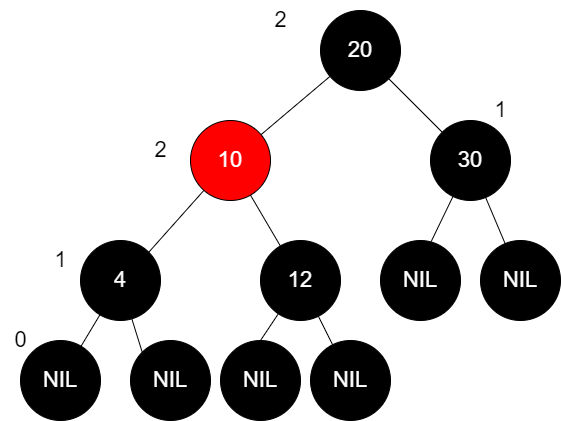
节点旁边的表示是对应的黑高。

红黑树通俗点，就是节点的左右子树高度差异不会很大，而上文提到的二叉搜索树的插入和删除，这两个会影响左右子树的高度差，因此我们要在插入或者删除后，调整红黑树的某些节点的左右子树，才能使得这两个操作满足红黑树的性质。

我们可以将红黑树中所有的NIL节点（包括根节点的双亲）都指向同一个，即：

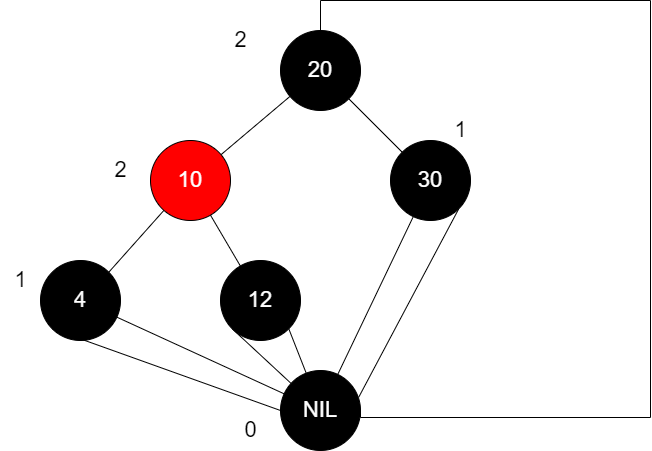
为了方便，我们可以对NIL节点进行缺省，即：

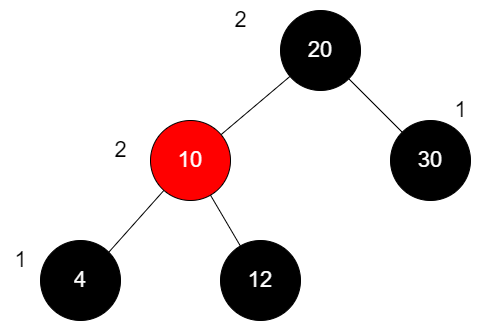
左旋右旋

在开始前，我们先来认识左旋右旋，这两个操作会辅助我们对红黑树调整：

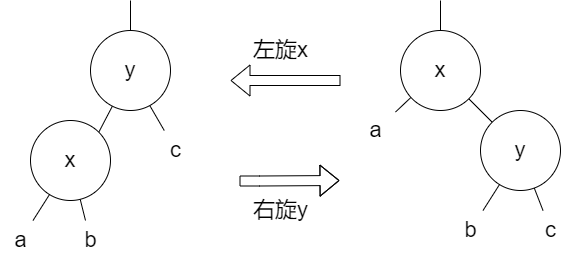
上述的左旋右旋是以最上层的结点角度来说的

左旋x节点：假设x节点的右孩子节点y不是NIL节点，则y成为该子树的新的根节点，x成为y的左孩子，y的左孩子成为x的右孩子。

左旋时，我们假定x.right!=NIL且根节点的父节点为T.NIL，则左旋的伪代码如下：

rb_tree_left_rotation(T, x){
    y = x.right;
    x.right = y.left;
    if y.left != T.NIL
        y.left.p = x;
    y.p = x.p;
    // 如果x是红黑树的根节点
    if x.p == T.NIL
        T.root = y;
    	T.root.p = T.NIL;
    // 如果x是双亲节点的左孩子
    else if x == x.p.left
        x.p.left = y;
    // 如果x是双亲节点的右孩子
    else
        x.p.right = y;
    y.left = x;
    x.p = y;
}

右旋时，我们假定y.left!=NIL，且根节点的父节点为T.NIL，则右旋的伪代码如下：

rb_tree_right_rotation(T, y){
    x = y.left;
    y.left = x.right;
    if x.right != T.NIL
        x.right.p = y;
    x.p = y.p;
    // 如果y是红黑树的根节点
    if y.p == T.NIL
        T.root = x;
    	T.root.p = T.NIL;
    // 如果y是双亲节点的左孩子
    else if y == y.p.left
        y.p.left = x;
    // 如果y是双亲节点的右孩子
    else
        y.p.right = x;
    x.right = y;
    y.p = x;
}

插入

插入步骤主要包括以下步骤：

1. 找到合适位置，插入节点
2. 将新节点染成红色
3. （可选的）调整红黑树，直至符合红黑树定义

与往二叉搜索树中插入节点类似：

rb_tree_insert(T, z){
    y = T.NIL;
    x = T.root;
    while x != T.NIL
        y = x;
      	// 插到左子树
      	if z.key < x.key
            x = x.left;
      	// 插到右子树
      	else
          	x = x.right;
    z.p = y;
    // 空树
    if y == T.NIL
        T.root = z;
    else if z.key < y.key
        y.left = z;
    else 
        y.right = z;
    z.left = T.NIL;
    z.right = T.NIL;
    z.color = RED;
    rb_tree_insert_fixup(T, z);
}

如果节点z插入的位置中，其双亲节点是黑色的，则无需进行调整，这是因为插入这个红色节点后并不会违反上文所提的5个性质，相反，如果其双亲节点是红色的，那么就有连续两个红色的节点，违反了性质4，这时候我们要对红黑树进行调整，我们可以证明，仅当新插入的节点的双亲是红色时，需要对红黑树调整，我们可以将需要进行调整的情况分为3种：

1. z的叔节点y是红色的。
2. z的叔节点y是黑色的且z是其双亲的右孩子。
3. z的叔节点y是黑色的且z是其双亲的左孩子。

在情况1中，由于y是红色的，我们可以同时将z的双亲和y染成黑色，将y的双亲染成红色，则以y的双亲为根的子树满足红黑树定义（当然如果y的双亲是整棵红黑树的根，则y的双亲要再次染成黑色的）。

由于y的双亲被染成了红色，有可能会对y的祖先造成影响（即此时y的双亲的双亲是红色的，此时存在连续的红色的节点），使得一些祖先不能满足红黑树定义，此时，我们要把y的双亲当成z，递归重新判断。

在情况2中，由于z是其双亲的右孩子，我们可以对z的双亲进行一次左旋，此时可以转为情况3.

在情况3中，由于z和z的双亲是红色的，则y的双亲必然是黑色的（因为插入z之前，树是满足红黑树定义的，而z的双亲是红色的，则z的双亲的双亲必然是黑色的），因此我们可以对z的双亲染成黑色，而y的双亲是红色，再对y的双亲做一个右旋，则以z的双亲为根的子树满足红黑树定义。

我们可以以算法导论中的例子为例：

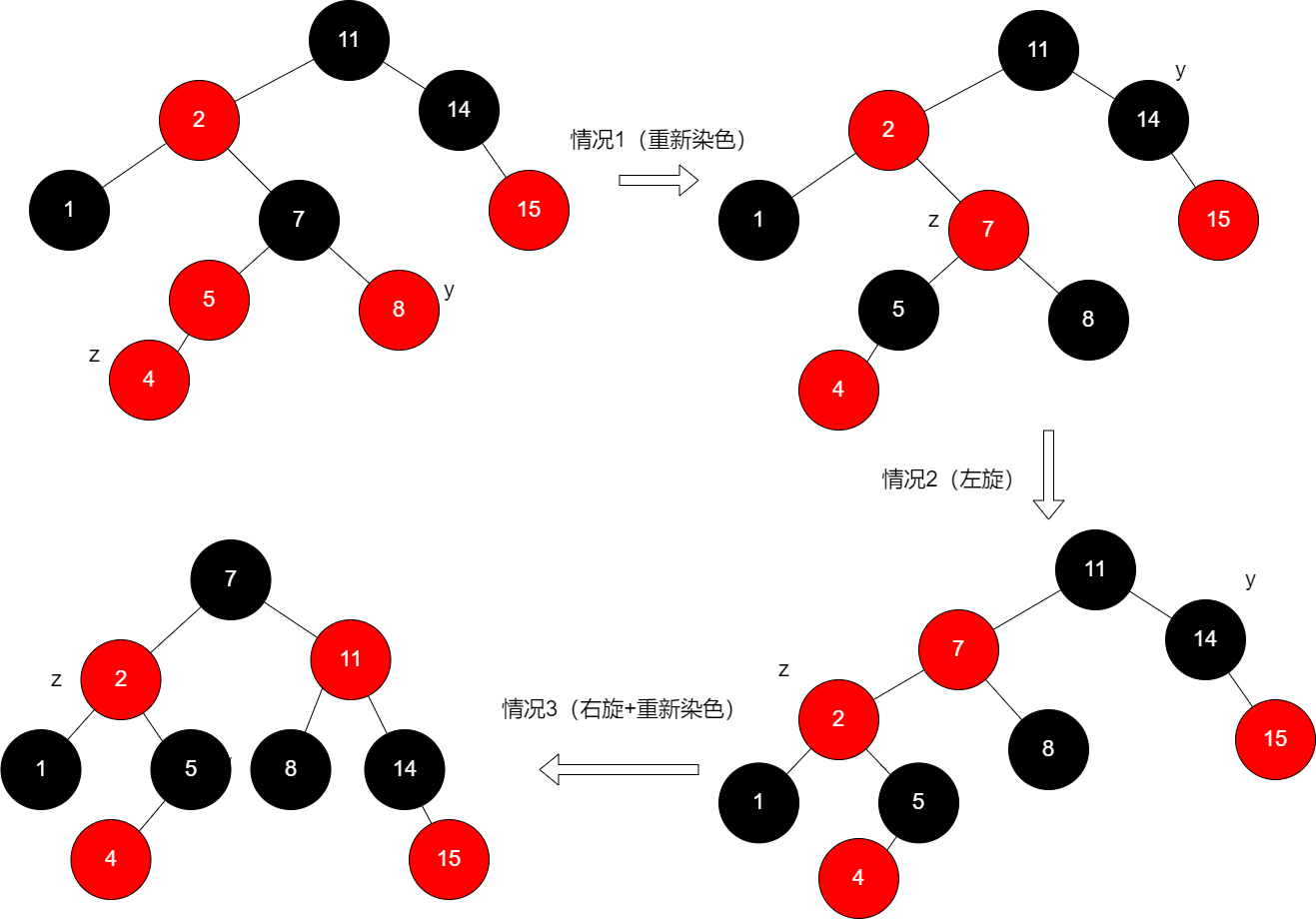
因此调整的伪代码为：

rb_tree_insert_fixup(T, z){
    while z.p.color == RED
        // 如果z的双亲是左孩子
        if z.p == z.p.p.left
            y = z.p.p.right;
            if y.color == RED
                z.p.color = BLACK;					// case 1
                y.color = BLACK;					// case 1
                z.p.p.color = RED;					// case 1
                z = z.p.p;							// case 1
            else if z == z.p.right
                z = z.p;							// case 2
                rb_tree_left_rotation(T, z)			// case 2
            else
                z.p.color = BLACK;					// case 3
                z.p.p.color = RED;					// case 3
                rb_tree_right_rotation(T, z.p.p);	// case 3
    	// 如果z的双亲是右孩子
    	else
            // 与上面分支对称，将left和right互换即可
            ...
    // 不管怎样，红黑树的性质2一定要满足
	T.root.color = BLACK;     
}

删除

删除过程有亿点点复杂，不过我们可以先分成几个大类（假设被删除的结点是z）：

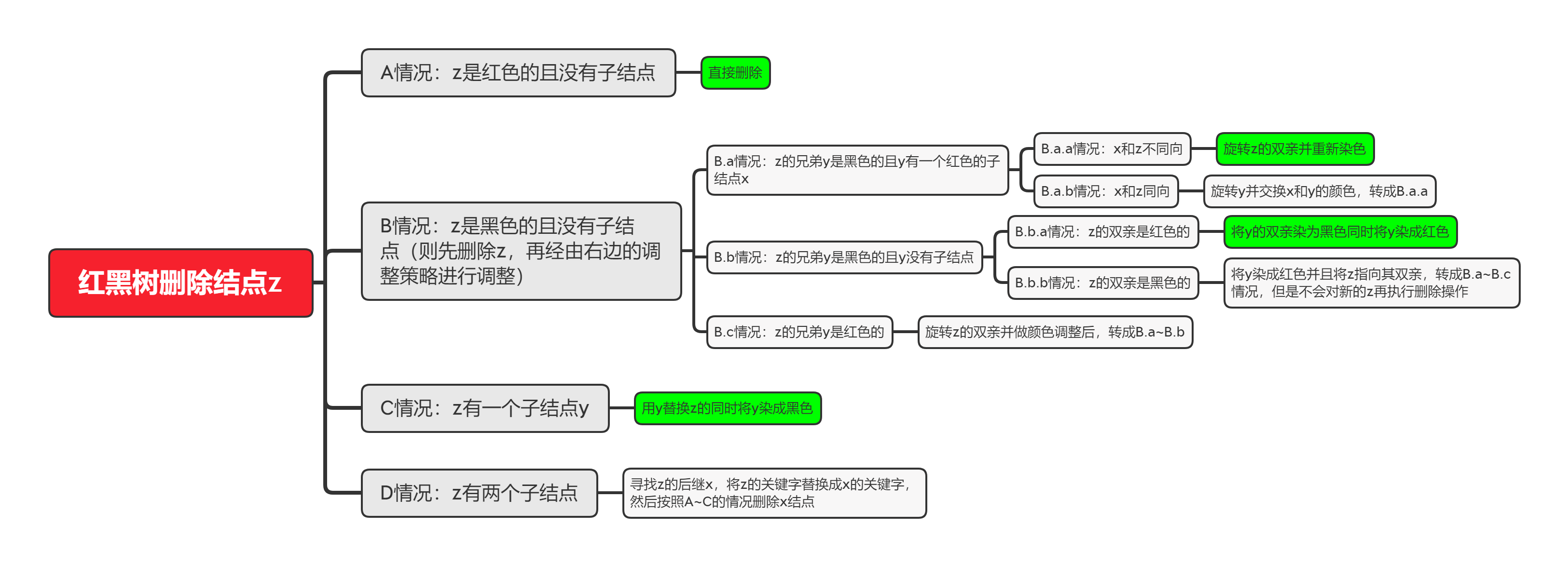
A.：z是红色的，且没有子结点：由于其没有孩子，因此删除这个红色结点对其子树（实际子树为空）以及其他的子树都不影响，我们简单地将其删除即可。

B.：z是黑色的，且没有子结点：由于z是黑色的，那么删除z后，对于之前简单路径中包含z的路径长度都减少了1，我们破坏了红黑树性质，这个分类是最复杂的，因此我们后面再展开这类。

C.：z只有一个非T.NIL子结点y：这种情况下，z必然是黑色的且y是红色的，为什么呢？假如z和y都是黑色的，那么根到y的子树的叶子节点的简单路径中黑色结点个数会比根到z的另一个空子树的叶子节点的简单路径中黑色结点个数多1，同理也不可能出现“z是红色的且y是黑色的”，这种情况下我们可以用y替换z（然后删除z），同时将y染成黑色即可。

D.：z有两个子结点：根据之前二叉搜索树的删除，我们可以知道，将来替换z的结点是z的后继x（实际上前驱也可以，不过我们延续二叉搜索树的做法），替换过程我们把z的关键字设置为x的关键字，然后我们删除x按照步骤A、B、C进行（因为x是z的后继，根据前面知识我们知道，当z存在右孩子时，其后继x是z的右子树中最左边的结点，因此其不可能有两个孩子结点）

我们重点展开B类情况：

开始之前，我们先思考一下，如果z是根节点，我们直接删除z即可，然后将红黑树根节点设置为T.NIL即可，如果z不是根节点，参照上文C类的分析，当z没有子结点且z是黑色的情况下，z必然存在一个兄弟节点，我们记该结点为y。

B.a：z的兄弟y是黑色的，且y有一个红色的子结点x，我们对y进行一次旋转，然后再重新染色，再删除z即可，这里又可以分为两种情况：

• B.a.a：x和z不同向，即一个为左节点，一个为右节点，当z是右节点时，我们对y的双亲进行右旋，如果z是左节点，我们则对y的双亲进行左旋，如下图所示：

  

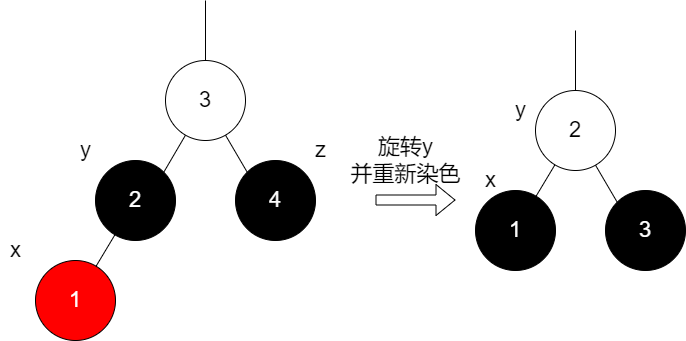
  注意，变化后新的2号结点颜色要与原先的3号节点颜色相同，否则不满足性质5；此外我们可以证明x没有非NIL子结点

• B.a.b：x和z同向，即同为其双亲的右孩子或者左孩子，此时我们可以旋转y，并交换x和y的颜色，即可转至上面B.a.a的情况: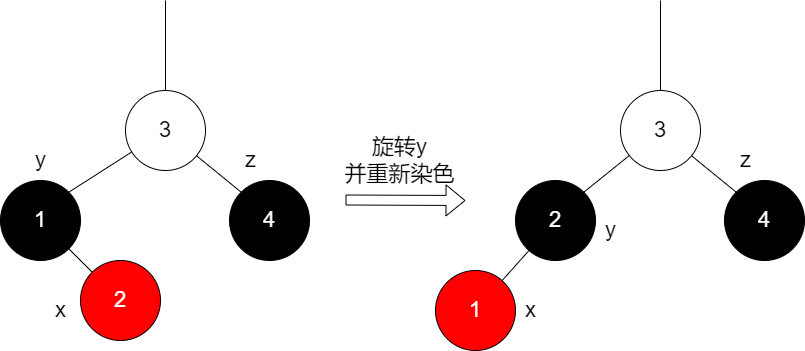

  

B.b：z的兄弟y是黑色的，且y没有子结点，这里可以分z的双亲是红色和黑色情况

• B.b.a：如果z的双亲是红色：这里比较简单，我们直接删除z，然后将y的双亲染为黑色同时将y染为红色

  

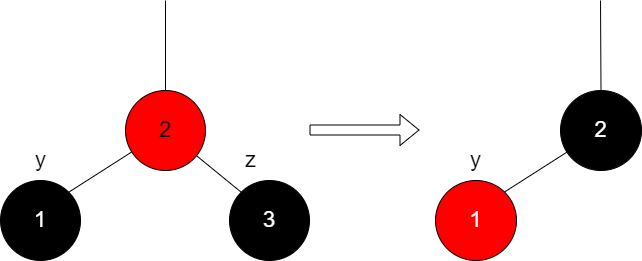
• B.b.b：如果z的双亲是黑色的，这种情况就比较复杂了，我们需要先删除z的同时将y染成红色，然后将z指向y的双亲，由于新的z只有一个红色的子结点y，红色结点的存在与否不影响包含该节点的简单路径中黑色结点个数，因此我们可以当成是B情况的特例，然后使用B.a~B.c的情况进一步调整（虽然B.c的情况在下面才说明），只不过有些时候我们把黑色的非NIL结点当成了NIL结点，但是不影响最终的调整，注意这种情况下我们不再对新的z进行删除操作。当然这个过程中，z有可能一直往上，直至遇到根节点，届时我们不再需要往上进行，这几种情况如下图所示：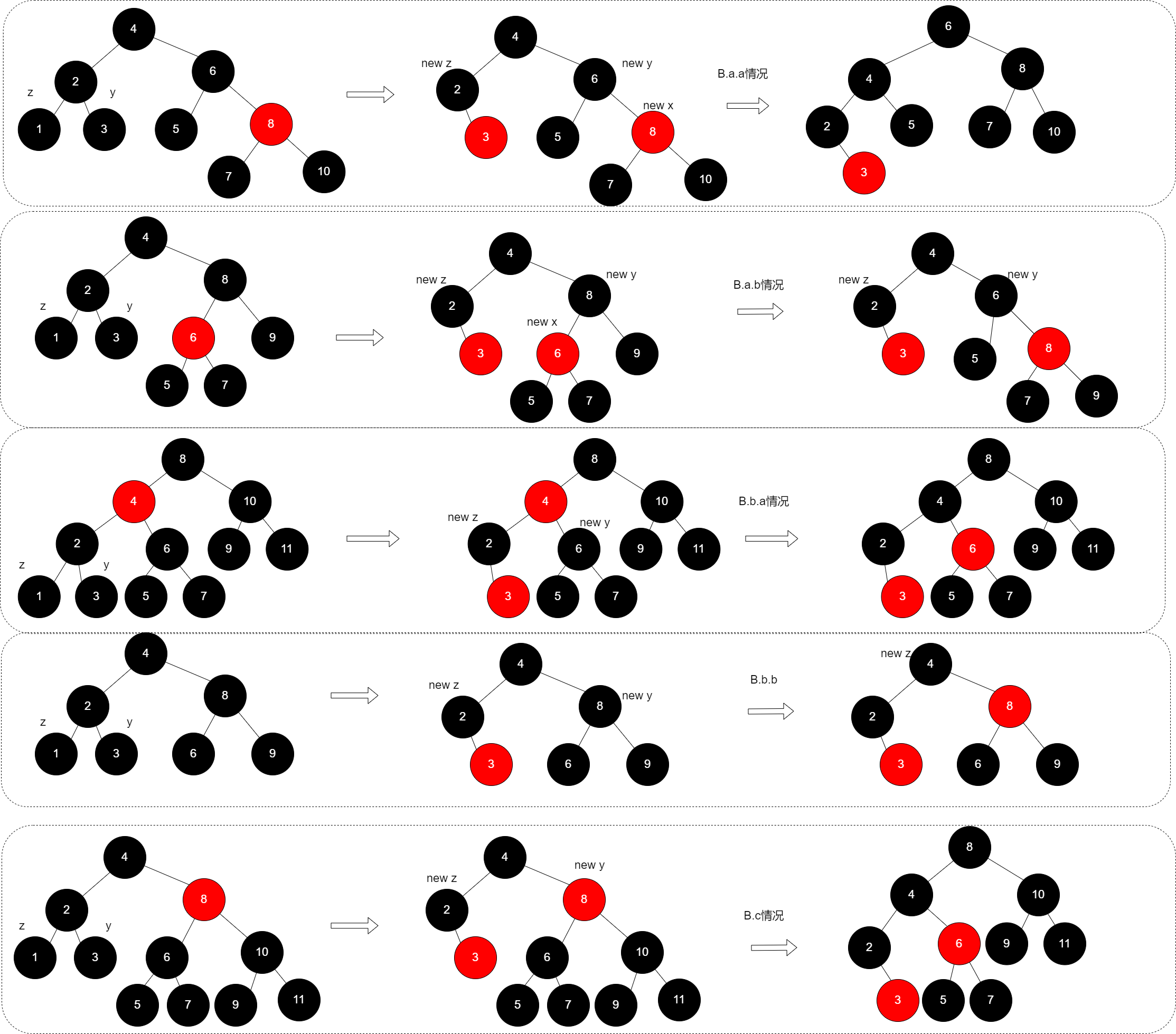

  

B.c：z的兄弟y是红色的，由于z是黑色的且没有子结点，y是红色的，因此z的双亲必然是黑色的且y有两个黑色的子结点（但是y有没有红色的孙子结点不确定）：

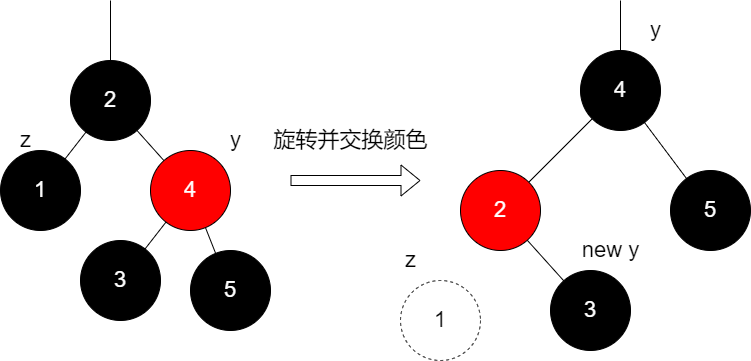
我们可以先对z的双亲做一个旋转（上图的情况是左旋，当z是右孩子时对称地对双亲右旋即可），并将y和其新的左孩子对调颜色，外面可以发现，此时如果不删除结点1，那么这棵树是满足红黑树的，但是外面删除了结点1，言外之意，我们把左边的删除过程和右边做了一个等价交换，而这种情况，我们可以转成B.a和B.b情况。

new y 和 旧的y同向

还有一点值得注意，B情况包含涵盖了所有情况了吗？？其实没有，我们还缺少一种情况，即“z是黑色的没有孩子结点，且z的兄弟结点y也是黑色的且y有两个红孩子”，但是我们这种情况可以规约成B.a.a情况，例如：

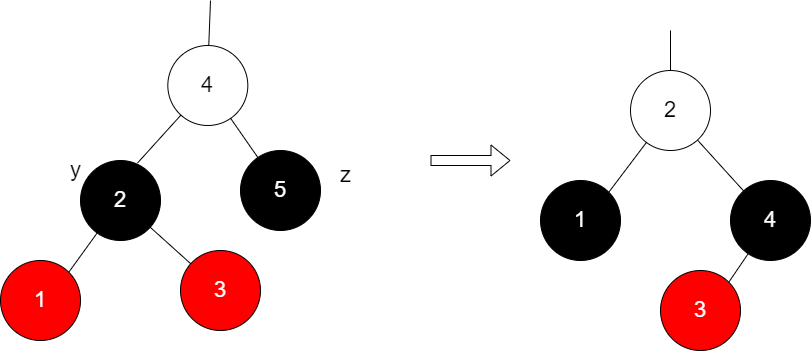
完成上面的分析后，我们就可以写出这部分的伪代码了，不过在开始之前，我们也要先定义一个子过程，用于使用以v为根的子树来替换以u为根的子树

rb_tree_transplant(T, u, v){
    if u.p == T.NIL
        T.root = v;
    else if u == u.p.left
        u.p.left = v;
    else
        u.p.right = v;
    v.p = u.p;
}

ok，下面是删除功能的伪代码了：

rb_tree_delete_case_B_a_a_fix(T, x){
    y = x.p;
    y_is_left = (y == y.p.left);
    y_p_color = y.p.color
    if y_is_left
        rb_tree_right_rotation(T, y.p)
    	y.right.color = BLACK;
    else
        rb_tree_left_rotation(T, y.p);
    	y.left.color = BLACK;
    x.color = BLACK;
    y.color = y_p_color;
}
rb_tree_delete_case_B_a_b_fix(T, x){
    y = x.p;
    y_is_left = (y == y.p.left);
    y.color = RED;
    x.color = BLACK
    if y_is_left
        rb_tree_left_rotation(T, y);
    else
        rb_tree_right_rotation(T, y);
    // 交换 x 和 y 指针
    swap_ptr(y, x);
    // 化为 B.a.a
    rb_tree_delete_case_B_a_a_fix(T, x);
}
yrb_tree_delete_case_B_b_a_fix(T, y){
    y.color = RED;
    y.p.color = BLACK;
}

rb_tree_delete_case_B_b_b_fix(T, y){
    y.color = RED;
    new_z = y.p;
    if new_z == T.root
        return;
    new_z_is_left = (new_z == new_z.p.left);
    new_y = (new_z_is_left ? new_z.p.right : new_z.p.left)
    if new_y.color == BLACK and (
        (new_z_is_left and new_y.right != T.NIL and new_y.right.color == RED) or 
        (!new_z_is_left and new_y.left != T.NIL and new_y.left.color == RED)
    )
        // 转 B.a.a后结束
        rb_tree_delete_case_B_a_a_fix(T, new_z_is_left ? new_y.right : new_y.left);
    else if new_y.color == BLACK and ( 
        (new_z_is_left and new_y.left != T.NIL and new_y.left.color == RED) or
        (!new_z_is_left and new_y.right != T.NIL and new_y.right.color == RED)
    )
        // 转 B.a.b后结束
        rb_tree_delete_case_B_a_a_fix(T, new_z_is_left ? new_y.left : new_y.right);
    // 注意，这里使用“y是不是有俩个黑色的子结点”而不是使用“y是不是有两个NIL子结点”
    else if new_y.color == BLACK and new_y.left.color == BALCK and new_y.right.color == BALCKL and new_z.p.color == RED
        // 转 B.b.a后结束
        rb_tree_delete_case_B_b_a_fix(T, new_y);
    else if new_y.color == BLACK and new_y.left.color == BALCK and new_y.right.color == BALCKL and new_z.p.color == BLACK
        // 继续递归 B.b.b
        rb_tree_delete_case_B_b_b_fix(T, new_y);
    else if new_y.color == RED
        // 转 B.c后结束
        rb_tree_delete_case_B_c_fix(T, new_y);
}
rb_tree_delete_case_B_c_fix(T, y){
    y.color = BLACK;
    y_is_left = (y == y.p.left);
    if y_is_left
        rb_tree_right_rotation(T, y.p);
    	y.right.left.color = RED;
    	new_y = y.right.left;
    else
        rb_tree_left_rotation(T, y.p);
		y.left.right.color = RED;
    	new_y = y.left.right;
    // 如果 new_y 有红色子结点，跳转 B.a.a 或者 B.a.b
    if (y_is_left and new_y.left.color == RED) or 
       (!y_is_left and new_y.right.color == RED)
        rb_tree_delete_case_B_a_a_fix(T, y_is_left ? new_y.left : new_y.right);
    else if (y_is_left and new_y.right.color == RED) or 
       (!y_is_left and new_y.left.color == RED)
        rb_tree_delete_case_B_a_b_fix(T, y_is_left ? new_y.right : new_y.left);
	 // 如果 new_y 有没有子结点，由于 new y 的双亲是红色的，跳转B.b.a
    else if new_y.left.color == BLACK and new_y.right.color == BLACK
        rb_tree_delete_case_B_b_a_fix(T, new_y);
}
rb_tree_delete_case_A(T, z){
    // 直接删除
    if z == z.p.left
        z.p.left = T.NIL;
    else
        z.p.right = T.NIL;
}
rb_tree_delete_case_B(T, z){
    
    // 先删除z
    if z == z.p.left
        z.p.left = T.NIL;
    	y = z.p.right;
    	z_is_left = true;
    else
        z.p.right = T.NIL;
    	y = z.p.left;
        z_is_left = false;
    // 如果z是根节点，则删除后是空树，不需要考虑z的兄弟节点了，因为根本不存在
    if z == T.root
        T.root = T.NIL;
        return;
    // 再根据不同的情况进行调整
    // b.a.a
    if y.color == BLACK and (
        (z_is_left and y.right != T.NIL and y.right.color == RED) or 
        (!z_is_left and y.left != T.NIL and y.left.color == RED)
    )
        rb_tree_delete_case_B_a_a_fix(T, z_is_left ? y.right : y.left);
    // b.a.b
    else if y.color == BLACK and ( 
        (z_is_left and y.left != T.NIL and y.left.color == RED) or
        (!z_is_left and y.right != T.NIL and y.right.color == RED)
    )
        rb_tree_delete_case_B_a_b_fix(T, z_is_left ? y.left : y.right);
    // b.b.a
    else if y.color == BLACK and y.left == T.NIL and y.right == T.NIL and z.p.color == RED
        rb_tree_delete_case_B_b_a_fix(T, y);
    // b.b.b
    else if y.color == BLACK and y.left == T.NIL and y.right == T.NIL and z.p.color == BLACK
        rb_tree_delete_case_B_b_b_fix(T, y);
    // b.c
    else if y.color == RED
        rb_tree_delete_case_B_c_fix(T, y);
}
rb_tree_delete_case_C(T, z){
    if z.left == T.NIL
        y = z.right;
    else
        y = z.left;
    rb_tree_transplant(T, z, y);
    y.color = BLACK;
}
rb_tree_delete_case_D(T, z){
    x = rb_tree_search_suc(z);
    z.key = x.key;
    rb_tree_delete(T, x);
}
rb_tree_delete(T, z){
    // A情况
    else if z.color == RED and z.left == T.NIL and z.right == z.left
        rb_tree_delete_case_A(T, z);
    // B情况
    else if z.color == BLACK and z.left == T.NIL and z.right == T.NIL
        rb_tree_delete_case_B(T, z);
    // C情况
    else if (z.left == T.NIL and z.right != T.NIL) or (z.right == T.NIL and z.left != T.NIL)
        rb_tree_delete_case_C(T, z);
    // D情况
    else if z.left != T.NIL and z.right != T.NIL
        rb_tree_delete_case_D(T, z);
}

C语言实现

先定义红黑树以及树的结点：

typedef struct Node {
    int key;
    int color;
    struct Node* p, * left, * right;
}TreeNode;

typedef struct Tree {
    TreeNode* root;
    TreeNode* NIL;
}RedBlackTree;

然后是初始化红黑树的代码：

// 初始化一个NIL结点，红黑树整个生命周期只会生成一个NIL结点
void initRedBlackTree(RedBlackTree* tree) {
    TreeNode* nil = (TreeNode*)malloc(sizeof(TreeNode));
    nil->color = BLACK;
    tree->NIL = nil;
    tree->root = nil;
    tree->root->p = tree->NIL;
    tree->root->left = tree->NIL;
    tree->root->right = tree->NIL;
}

我们还要写一个用于验证红黑树的函数：

int valid;
int dfsValid(RedBlackTree* T, TreeNode* root, TreeNode* p) {
    if (root->color != RED && root->color != BLACK) {
        // 性质1
        valid = -1;
    }
    if (root == T->NIL && root->color != BLACK) {
        // 性质3
        valid = -1;
    }
    if (root->color == RED && (root->left->color == RED || root->right->color == RED)) {
        // 性质4
        valid = -1;
    }
    if (root != T->NIL && root->p != p) {
        valid = -1;
    }
    // 性质5
    if (root != T->NIL) {
        int leftBlackNodeCnt = dfsValid(T, root->left, root);
        int rightBlackNodeCnt = dfsValid(T, root->right, root);
        if (leftBlackNodeCnt != rightBlackNodeCnt) {
            valid = -1;
        }
        return leftBlackNodeCnt + (root->color == BLACK ? 1 : 0);
    }

    // 搜索树性质
    if (root->left != T->NIL && root->left->key > root->key) {
        valid = -1;
    }
    if (root->right != T->NIL && root->right->key < root->key) {
        valid = -1;
    }
    return (root->color == BLACK ? 1 : 0);
}




int redBlackTreeValid(RedBlackTree* T) {
    // 根节点是黑色的（性质2），空节点是黑色的（性质3）
    if (T->root->color != BLACK || T->NIL->color != BLACK) {
        return -1;
    }
    if (T->root->p != T->NIL) {
        return -1;
    }
    valid = 1;
    dfsValid(T, T->root, T->NIL);
    if (valid == -1) {
        printf("*********Not valid red black tree!*********\n");
        return -1;
    }
    return 1;
}

我们可以编写一个测试代码，测试10次，每次产生指定长度10000的随机数据插入，插入完毕后随机删除结点：

int final_test(int len, int debug) {

    if (len > 10000) {

    }
    RedBlackTree* T = (RedBlackTree*)malloc(sizeof(RedBlackTree));
    initRedBlackTree(T);
    redBlackTreeValid(T);

    int nums[10000];
    // 测试插入
    printf("----- start insert  -----\n");
    for (int i = 0; i < len;i++) {
        nums[i] = generateRandomNumber(0, len);
        if (debug) {
            printf("insert %d\n", nums[i]);
        }
        TreeNode* z = (TreeNode*)malloc(sizeof(TreeNode));
        z->color = RED;
        z->p = T->NIL;
        z->left = T->NIL;
        z->right = T->NIL;
        z->key = nums[i];
        rb_tree_insert(T, z);
        redBlackTreeValid(T);
    }
    // 测试删除
    printf("----- start delete  -----\n");
    int remain = len;
    int deleteIdx, deleteKey;
    for (int i = 1; i <= len;i++) {
        deleteIdx = generateRandomNumber(0, remain);
        // 避免下次再被选到
        deleteKey = nums[deleteIdx];
        // printf("delete %d\n", deleteKey);
        nums[deleteIdx] = nums[remain - 1];
        nums[remain - 1] = deleteKey;
        TreeNode* z = rb_tree_search(T, T->root, deleteKey);

        if (z == T->NIL) {
            printf("No found!");
        }
        else {
            if (debug) {
                printf("delete %d\n", deleteKey);
            }
            rb_tree_delete(T, z);
            if (redBlackTreeValid(T) == -1) {
                printf("delete error just now on %d\n", deleteKey);
            }
        }

        remain--;

    }

}
int main() {
    // 重新设置随机数种子
    srand(time(NULL));
    for (int i = 1; i <= 10; i++) {
        final_test(10000, 0);
    }
    return 0;
}

测试结果如下（如果有出现删除或者插入后不符合红黑树性质，则会打印*********Not valid red black tree!*********）

完整实现：

#include<stdio.h>
#include<malloc.h>
#include <stdlib.h>
#include <time.h>
#define RED 0
#define BLACK 1
typedef struct Node {
    int key;
    int color;
    struct Node* p, * left, * right;
}TreeNode;

typedef struct Tree {
    TreeNode* root;
    TreeNode* NIL;
}RedBlackTree;
// 初始化一个NIL结点，红黑树整个生命周期只会生成一个NIL结点
void initRedBlackTree(RedBlackTree* tree) {
    TreeNode* nil = (TreeNode*)malloc(sizeof(TreeNode));
    nil->color = BLACK;
    tree->NIL = nil;
    tree->root = nil;
    tree->root->p = tree->NIL;
    tree->root->left = tree->NIL;
    tree->root->right = tree->NIL;
}
void rb_tree_left_rotation(RedBlackTree* T, TreeNode* x) {
    TreeNode* y = x->right;
    x->right = y->left;
    if (y->left != T->NIL) {
        y->left->p = x;
    }
    y->p = x->p;
    // 如果x是红黑树的根节点
    if (x->p == T->NIL) {
        T->root = y;
        T->root->p = T->NIL;
    }
    // 如果x是双亲节点的左孩子
    else if (x == x->p->left) {
        x->p->left = y;
    }
    // 如果x是双亲节点的右孩子
    else {
        x->p->right = y;
    }
    y->left = x;
    x->p = y;
}
void rb_tree_right_rotation(RedBlackTree* T, TreeNode* y) {
    TreeNode* x = y->left;
    y->left = x->right;
    if (x->right != T->NIL) {
        x->right->p = y;
    }
    x->p = y->p;
    // 如果y是红黑树的根节点
    if (y->p == T->NIL) {
        T->root = x;
        T->root->p = T->NIL;
    }
    // 如果y是双亲节点的左孩子
    else if (y == y->p->left) {
        y->p->left = x;
    }
    // 如果y是双亲节点的右孩子
    else {
        y->p->right = x;
    }
    x->right = y;
    y->p = x;
}

TreeNode* rb_tree_search(RedBlackTree* T, TreeNode* root, int key) {

    if (root == T->NIL || root->key == key) {
        return root;
    }
    // 在左子树中
    if (key < root->key) {
        return rb_tree_search(T, root->left, key);
    }
    // 在右子树中
    else {
        return rb_tree_search(T, root->right, key);
    }
}
// ======= 插入开始部分  ==========
void rb_tree_insert_fixup(RedBlackTree* T, TreeNode* z) {
    TreeNode* y;
    while (z->p->color == RED) {
        // 如果z的双亲是左孩子
        if (z->p == z->p->p->left) {
            y = z->p->p->right;
            if (y->color == RED) {
                z->p->color = BLACK;				// case 1
                y->color = BLACK;				    // case 1
                z->p->p->color = RED;				// case 1
                z = z->p->p;                        // case 1
            }
            else if (z == z->p->right) {
                z = z->p;                           // case 2
                rb_tree_left_rotation(T, z);		// case 2
            }
            else {
                z->p->color = BLACK;				// case 3
                z->p->p->color = RED;				// case 3
                rb_tree_right_rotation(T, z->p->p);	// case 3
            }
        }
        else {
            y = z->p->p->left;
            if (y->color == RED) {
                z->p->color = BLACK;				// case 1
                y->color = BLACK;				    // case 1
                z->p->p->color = RED;				// case 1
                z = z->p->p;                        // case 1
            }
            else if (z == z->p->left) {
                z = z->p;                           // case 2
                rb_tree_right_rotation(T, z);		// case 2
            }
            else {
                z->p->color = BLACK;				// case 3
                z->p->p->color = RED;				// case 3
                rb_tree_left_rotation(T, z->p->p);	// case 3
            }
        }
    }
    // 不管怎样，红黑树的性质2一定要满足
    T->root->color = BLACK;
}


void rb_tree_insert(RedBlackTree* T, TreeNode* z) {
    TreeNode* y = T->NIL;
    TreeNode* x = T->root;
    while (x != T->NIL) {
        y = x;
        // 插到左子树
        if (z->key < x->key) {
            x = x->left;
        }
        // 插到右子树
        else {
            x = x->right;
        }
    }
    z->p = y;
    // 空树
    if (y == T->NIL) {
        T->root = z;
    }
    else if (z->key < y->key) {
        y->left = z;
    }
    else {
        y->right = z;
    }
    z->left = T->NIL;
    z->right = T->NIL;
    z->color = RED;
    rb_tree_insert_fixup(T, z);
}

// ======= 插入结束部分  ==========


// ======= 删除开始部分  ==========
rb_tree_delete_case_B_a_a_fix(RedBlackTree* T, TreeNode* x) {
    TreeNode* y = x->p;
    int y_is_left = (y == y->p->left);
    int y_p_color = y->p->color;
    if (y_is_left) {
        rb_tree_right_rotation(T, y->p);
        y->right->color = BLACK;
    }
    else {
        rb_tree_left_rotation(T, y->p);
        y->left->color = BLACK;
    }
    x->color = BLACK;
    y->color = y_p_color;
}
rb_tree_delete_case_B_a_b_fix(RedBlackTree* T, TreeNode* x) {
    TreeNode* y = x->p;
    int y_is_left = (y == y->p->left);
    y->color = RED;
    x->color = BLACK;
    if (y_is_left) {
        rb_tree_left_rotation(T, y);
    }
    else {
        rb_tree_right_rotation(T, y);
    }
    // 交换 x 和 y 指针
    TreeNode* t = x;
    x = y;
    y = t;
    // 化为 B->a->a
    rb_tree_delete_case_B_a_a_fix(T, x);
}
rb_tree_delete_case_B_b_a_fix(RedBlackTree* T, TreeNode* y) {
    y->color = RED;
    y->p->color = BLACK;
}
rb_tree_delete_case_B_c_fix(RedBlackTree* T, TreeNode* y) {
    y->color = BLACK;                     
    int y_is_left = (y == y->p->left);
    TreeNode* new_y;
    if (y_is_left) {
        rb_tree_right_rotation(T, y->p);
        y->right->color = RED;
        new_y = y->right->left;
    }
    else {
        rb_tree_left_rotation(T, y->p);
        y->left->color = RED;
        new_y = y->left->right;
    }
    // new_y 和旧的 y 是同向的
    // 如果 new_y 有红色子结点，跳转B.a.a 或者 B.a.b
    if ((y_is_left && new_y->left->color == RED) || (!y_is_left && new_y->right->color == RED)) {
        rb_tree_delete_case_B_a_a_fix(T, y_is_left ? new_y->left : new_y->right);
    }
    else if ((y_is_left && new_y->right->color == RED) || (!y_is_left && new_y->left->color == RED)) {
        rb_tree_delete_case_B_a_b_fix(T, y_is_left ? new_y->right : new_y->left);
    }
    // 如果 new_y 有没有子结点，由于 new y 的双亲是红色的，跳转B.b.a
    else if (new_y->left->color == BLACK && new_y->right->color == BLACK) {
        rb_tree_delete_case_B_b_a_fix(T, new_y);
    }

}
rb_tree_delete_case_B_b_b_fix(RedBlackTree* T, TreeNode* y) {
    y->color = RED;
    TreeNode* new_z = y->p;
    if (new_z == T->root) {
        return;
    }
    int new_z_is_left = (new_z == new_z->p->left);
    TreeNode* new_y = (new_z_is_left ? new_z->p->right : new_z->p->left);
    if (new_y->color == BLACK && (
        (new_z_is_left && new_y->right != T->NIL && new_y->right->color == RED) ||
        (!new_z_is_left && new_y->left != T->NIL && new_y->left->color == RED)
        )) {
        // 转 B.a.a后结束
        rb_tree_delete_case_B_a_a_fix(T, new_z_is_left ? new_y->right : new_y->left);
    }
    else if (new_y->color == BLACK && (
        (new_z_is_left && new_y->left != T->NIL && new_y->left->color == RED) ||
        (!new_z_is_left && new_y->right != T->NIL && new_y->right->color == RED)
        )) {
        // 转 B.a.b后结束
        rb_tree_delete_case_B_a_b_fix(T, new_z_is_left ? new_y->left : new_y->right);
    }
    // 注意，这里使用“y是不是有俩个黑色的子结点”而不是使用“y是不是有两个NIL子结点”
    else if (new_y->color == BLACK && new_y->left->color == BLACK && new_y->right->color == BLACK && new_z->p->color == RED) {
        // 转 B.b.a后结束
        rb_tree_delete_case_B_b_a_fix(T, new_y);
    }
    else if (new_y->color == BLACK && new_y->left->color == BLACK && new_y->right->color == BLACK && new_z->p->color == BLACK) {
        // 继续递归 B.b.b
        rb_tree_delete_case_B_b_b_fix(T, new_y);
    }
    else if (new_y->color == RED) {
        // 转 B.c后结束
        rb_tree_delete_case_B_c_fix(T, new_y);
    }
}

rb_tree_delete_case_A(RedBlackTree* T, TreeNode* z) {
    // 直接删除
    if (z == z->p->left) {
        z->p->left = T->NIL;
    }
    else {
        z->p->right = T->NIL;
    }
    free(z);
}
rb_tree_delete_case_B(RedBlackTree* T, TreeNode* z) {
    int z_is_left;
    TreeNode* y;
    // 先删除z
    if (z == z->p->left) {
        z->p->left = T->NIL;
        y = z->p->right;
        z_is_left = 1;
    }
    else {
        z->p->right = T->NIL;
        y = z->p->left;
        z_is_left = 0;
    }
    // 如果z是根节点，则删除后是空树，不需要考虑z的兄弟节点了，因为根本不存在
    if (z == T->root) {
        T->root = T->NIL;
        return;
    }
    TreeNode* z_p = z->p;
    free(z);

    // 其他再根据不同的情况进行调整
    // b.a.a
    if (y->color == BLACK && (
        (z_is_left && y->right != T->NIL && y->right->color == RED) ||
        (!z_is_left && y->left != T->NIL && y->left->color == RED)
        )) {
        rb_tree_delete_case_B_a_a_fix(T, z_is_left ? y->right : y->left);
    }
    // b.a.b
    else if (y->color == BLACK && (
        (z_is_left && y->left != T->NIL && y->left->color == RED) ||
        (!z_is_left && y->right != T->NIL && y->right->color == RED)
        )) {
        rb_tree_delete_case_B_a_b_fix(T, z_is_left ? y->left : y->right);
    }
    // b.b.a
    else if (y->color == BLACK && y->left == T->NIL && y->right == T->NIL && z_p->color == RED) {
        rb_tree_delete_case_B_b_a_fix(T, y);
    }
    // b.b.b
    else if (y->color == BLACK && y->left == T->NIL && y->right == T->NIL && z_p->color == BLACK) {
        rb_tree_delete_case_B_b_b_fix(T, y);
    }
    // b.c
    else if (y->color == RED) {
        rb_tree_delete_case_B_c_fix(T, y);
    }
}
rb_tree_transplant(RedBlackTree* T, TreeNode* u, TreeNode* v) {
    if (u->p == T->NIL) {
        T->root = v;
    }
    else if (u == u->p->left) {
        u->p->left = v;
    }
    else {
        u->p->right = v;
    }
    v->p = u->p;
}
rb_tree_delete_case_C(RedBlackTree* T, TreeNode* z) {
    TreeNode* y;
    if (z->left == T->NIL) {
        y = z->right;
    }
    else {
        y = z->left;
    }
    rb_tree_transplant(T, z, y);
    y->color = BLACK;
    free(z);
}
TreeNode* b_tree_search_min(RedBlackTree* T, TreeNode* root) {
    if (root == T->NIL) {
        return T->NIL;
    }
    TreeNode* ans = root;
    while (ans->left != T->NIL) {
        ans = ans->left;
    }
    return ans;
}
TreeNode* rb_tree_search_suc(RedBlackTree* T, TreeNode* x) {
    if (x->right != T->NIL) {
        return b_tree_search_min(T, x->right);
    }
    TreeNode* y = x->p;
    while (y != T->NIL && x == y->right) {
        x = y;
        y = y->p;
    }
    return y;
}
rb_tree_delete_case_D(RedBlackTree* T, TreeNode* z) {
    TreeNode* x = rb_tree_search_suc(T, z);
    z->key = x->key;
    rb_tree_delete(T, x);
}
rb_tree_delete(RedBlackTree* T, TreeNode* z) {
    // A情况
    if (z->color == RED && z->left == T->NIL && z->right == z->left) {
        rb_tree_delete_case_A(T, z);
    }
    // B情况
    else if (z->color == BLACK && z->left == T->NIL && z->right == T->NIL) {
        rb_tree_delete_case_B(T, z);
    }
    // C情况
    else if ((z->left == T->NIL && z->right != T->NIL) || (z->right == T->NIL && z->left != T->NIL)) {
        rb_tree_delete_case_C(T, z);
    }
    // D情况
    else if (z->left != T->NIL && z->right != T->NIL) {
        rb_tree_delete_case_D(T, z);
    }
}
// ======= 删除结束部分  ==========

int valid;
int dfsValid(RedBlackTree* T, TreeNode* root, TreeNode* p) {
    if (root->color != RED && root->color != BLACK) {
        // 性质1
        valid = -1;
    }
    if (root == T->NIL && root->color != BLACK) {
        // 性质3
        valid = -1;
    }
    if (root->color == RED && (root->left->color == RED || root->right->color == RED)) {
        // 性质4
        valid = -1;
    }
    if (root != T->NIL && root->p != p) {
        valid = -1;
    }
    // 性质5
    if (root != T->NIL) {
        int leftBlackNodeCnt = dfsValid(T, root->left, root);
        int rightBlackNodeCnt = dfsValid(T, root->right, root);
        if (leftBlackNodeCnt != rightBlackNodeCnt) {
            valid = -1;
        }
        return leftBlackNodeCnt + (root->color == BLACK ? 1 : 0);
    }

    // 搜索树性质
    if (root->left != T->NIL && root->left->key > root->key) {
        valid = -1;
    }
    if (root->right != T->NIL && root->right->key < root->key) {
        valid = -1;
    }
    return (root->color == BLACK ? 1 : 0);
}




int redBlackTreeValid(RedBlackTree* T) {
    // 根节点是黑色的（性质2），空节点是黑色的（性质3）
    if (T->root->color != BLACK || T->NIL->color != BLACK) {
        return -1;
    }
    if (T->root->p != T->NIL) {
        return -1;
    }
    valid = 1;
    dfsValid(T, T->root, T->NIL);
    if (valid == -1) {
        printf("*********Not valid red black tree!*********\n");
        return -1;
    }
    return 1;
}
// 生成[a, b)范围内的随机整数
int generateRandomNumber(int a, int b) {
    return a + rand() % (b - a);
}
void printdfs(RedBlackTree* T, TreeNode* root) {
    if (root == T->NIL) {
        return;
    }
    printf("%d:%c left = %d, right = %d\n", root->key, root->color == RED ? 'R' : 'B', root->left->key, root->right->key);
    printdfs(T, root->left);
    printdfs(T, root->right);
}
int final_test(int len, int debug) {

    if (len > 10000) {

    }
    RedBlackTree* T = (RedBlackTree*)malloc(sizeof(RedBlackTree));
    initRedBlackTree(T);
    redBlackTreeValid(T);

    int nums[10000];
    // 测试插入
    printf("----- start insert  -----\n");
    for (int i = 0; i < len;i++) {
        nums[i] = generateRandomNumber(0, len);
        if (debug) {
            printf("insert %d\n", nums[i]);
        }
        TreeNode* z = (TreeNode*)malloc(sizeof(TreeNode));
        z->color = RED;
        z->p = T->NIL;
        z->left = T->NIL;
        z->right = T->NIL;
        z->key = nums[i];
        rb_tree_insert(T, z);
        redBlackTreeValid(T);
    }
    // 测试删除
    printf("----- start delete  -----\n");
    int remain = len;
    int deleteIdx, deleteKey;
    for (int i = 1; i <= len;i++) {
        deleteIdx = generateRandomNumber(0, remain);
        // 避免下次再被选到
        deleteKey = nums[deleteIdx];
        // printf("delete %d\n", deleteKey);
        nums[deleteIdx] = nums[remain - 1];
        nums[remain - 1] = deleteKey;
        TreeNode* z = rb_tree_search(T, T->root, deleteKey);

        if (z == T->NIL) {
            printf("No found!");
        }
        else {
            if (debug) {
                printf("delete %d\n", deleteKey);
            }
            rb_tree_delete(T, z);
            if (redBlackTreeValid(T) == -1) {
                printf("delete error just now on %d\n", deleteKey);
            }
        }

        remain--;

    }

}
int main() {
    
    // 重新设置随机数种子
    srand(time(NULL));
    for (int i = 1; i <= 10; i++) {
        final_test(9999, 0);
    }



    return 0;
}

后记

红黑树可以称得上几乎平衡的二叉搜索树，能够在最坏的情况下把插入、检索和删除的时间复杂度都控制在$O(\lg(n))$，如果把一系列数据结构都当成是学生的话，把插入、随机检索和删除作为考核科目，那么红黑树可以比喻成每科都能拿90分的学霸，而二叉平衡树（AVL）在“检索”拿到95分，哈希表更是在“检索”科目拿到97分，不过后面两位学生在插入和删除方面拿到的分数就比90分低多了。

红黑树应用十分广，因为它能够做到插入、删除和检索都接近$O(\log n)$，没有平衡二叉树调整那么频繁，却能够接近平衡二叉树的查询时间，当然由于其树型结构，当面临大量顺序读写时，比不上数组，因为数组能够借助硬件缓存，使得CPU直接从高速缓存中拿到数据，而红黑树难以做到高命中率。在随机读写方面，除了哈希表，红黑树和平衡二叉树天下无敌！

参考文献

算法导论第三版