手撕红黑树！使用C语言带你实现一个平衡搜索树【前夕】

前言

红黑树是二叉搜索树中的一种，只不过增加了一个性质“在所有的叶子到根的路径中，没有一条路径会比其他路径长出2倍”，因此，可以保证最坏情况下基本动态集合操作（例如删除节点、插入节点和查找节点）的时间复杂度为O(lg n)，本篇是第一部分，二叉搜索树。

二叉搜索树

既然红黑树是二叉搜索树，我们先来认识一下二叉搜索树，顾名思义，二叉搜索树就是使用二叉树实现的便于搜索的树型数据结构，对于每个节点x，其左子树中的最大关键字不超过x.key，而右子树中的最小关键字不小于x.key，二叉搜索树除了指向左右孩子节点的指针外，还有指向双亲节点的指针p，根节点是唯一没有双亲节点指针的节点，每个节点的左右子树的节点都递归地满足上述条件。

二叉搜索树的插入、删除和访问的时间复杂度是$O(\lg n)$

后文简称二叉搜索树为搜索树

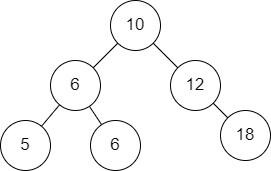
关于搜索树，我们有一个很重要的特点：

• 对搜索树进行中序遍历，可以得到一个非递减顺序

例如，上述中序遍历结果为：

5 6 6 10 12 18

查询指定关键字

从给定的搜索树root中查找关键字为k的节点，如果没有该节点，则返回NIL：

b_tree_search(root, k){
    if root == NIL or roor.key == k then
        return root
    // 在左子树中
    if k < root.key then
        return b_tree_search(root.left, k)
    // 在右子树中
    else
        return b_tree_search(root.right, k)
}

当然，为了提高效率，我们可以通过迭代的方式进行查找：

b_tree_search(root, k){
    while root != NIL and root.key != k
    // 在左子树中
    if k < root.key then
        root = root.left
    // 在右子树中
    else
        root = root.right
    return root
}

查询最大关键字或者最小关键字

根据搜索树的定义，我们很容易得出最小关键字的节点在最下角，最大关键字的节点在最右下角:

b_tree_search_min(root){
    if root == NIL then
        return NIL
    while root.left != NIL then
    	root = root.left
    return root
}

b_tree_search_max(root){
    if root == NIL then
        return NIL
    while root.right != NIL then
    	root = root.right
    return root
}

前驱和后继

如果搜索树中的关键字都不相同，那么对于搜索树的中序遍历得到的序列，则对于每一个非最小和最大关键字节点都有唯一前驱和后继，最小关键字节点没有前驱，最大关键字没有后继。

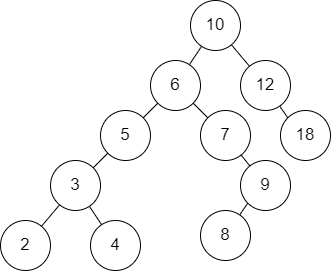
• 对于前驱，如果某个节点root的左孩子节点不空，则左孩子节点中最大关键字节点必然是root的前驱，例如节点5的左孩子不空，左孩子中最大关键字节点是4，4是5的前驱；如果左孩子是空，情况有些复杂，实际上如果x节点存在一个前驱y，则y在x的祖先集合中，并且是处于最低的，同时要求y有一个右孩子且该右孩子也在x的祖先集合中，因此我们可以从x开始沿着树网上，然后找到一个其双亲有右孩子的节点，例如对于节点8，前驱是7：

  b_tree_search_pre(x){
      if x.left != NIL then
          return b_tree_search_max(x.left)
      y = x.p
      while y != NIL and x == y.left then
          x = y
          y = y.p
      return y
  }
  

• 同理可得后继:

  b_tree_search_suc(x){
      if x.right != NIL then
          return b_tree_search_min(x.right)
      y = x.p
      while y != NIL and x == y.right then
          x = y
          y = y.p
      return y
  }
  

插入和删除

插入和删除会修改树和相应节点。

对于插入，输入搜索树T和待插入的节点z，其中z.key=v,z.left=NIL,z.right=NIL，插入操作主要是将节点放置于正确位置，同时新的树仍然满足搜索树的性质，插入过程，如果T是空树，则T的根指向z节点，然后直接返回即可，如果T不是空树，则从根节点开始，如果z节点关键字小于当前节点，则说明应该插到左子树中，相反，如果大于等于，则插入到右子树中，在左右子树中仍然以同样的思路进行，直到找到一个左子树为空（对应于要插入到左子树中的情况），或者直到找到一个右子树为空（对应于要插入到右子树中的情况），对应的伪代码为：

b_tree_search_insert(T, z){
    y = NIL;
    x = T.root;
    while x != NIL then
        y = x;
    	// 插到左子树
    	if z.key < x.key then
            x = x.left;
    	// 插到右子树
    	else
			x = x.right;
    z.p = y;
    // 空树
    if y == NIL then
        T.root = z
    else if z.key < y.key then
        y.left = z
    else then
        y.right = z
}

对于从树中删除z节点，情况比较复杂一些，但是大体可以分为以下几种情况（图中实线代表孩子，虚线代表子树）：

情况1. 如果z没有左孩子节点（图a），则使用右孩子直接替换z，右孩子可以为NIL 情况2. 如果z仅有一个孩子且该孩子是左孩子（图b），则使用左孩子直接替换z 再者. 如果z存在两个孩子时，我们需要寻该z的后继y（当然前驱也可以，我们这里使用后继），y一定是在右子树上（根据前面寻找后继的知识，我们可以知道y一定没有左孩子），我们用y替换z，同时对y的子树做一定调整，具体如下两个情况 情况3. 如果y是z的右孩子（图c），我们用y替换z，同时将z原先的左孩子设置为y的左孩子，y的右孩子不变。 情况4. 如果y不是z的右孩子（图d），我们先用y的右孩子替换y，再用y替换z

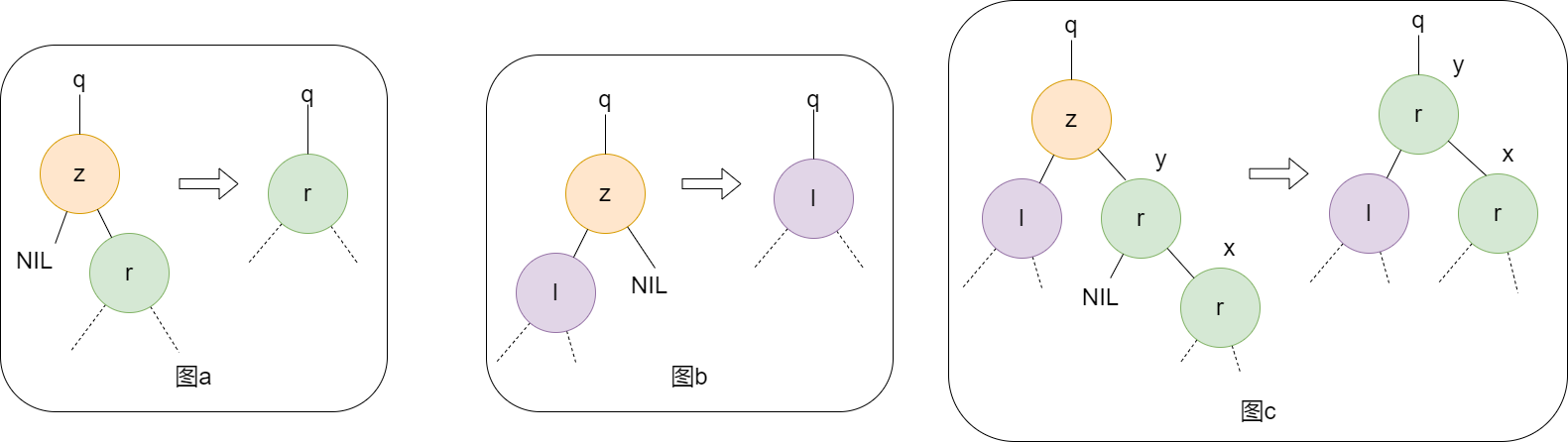
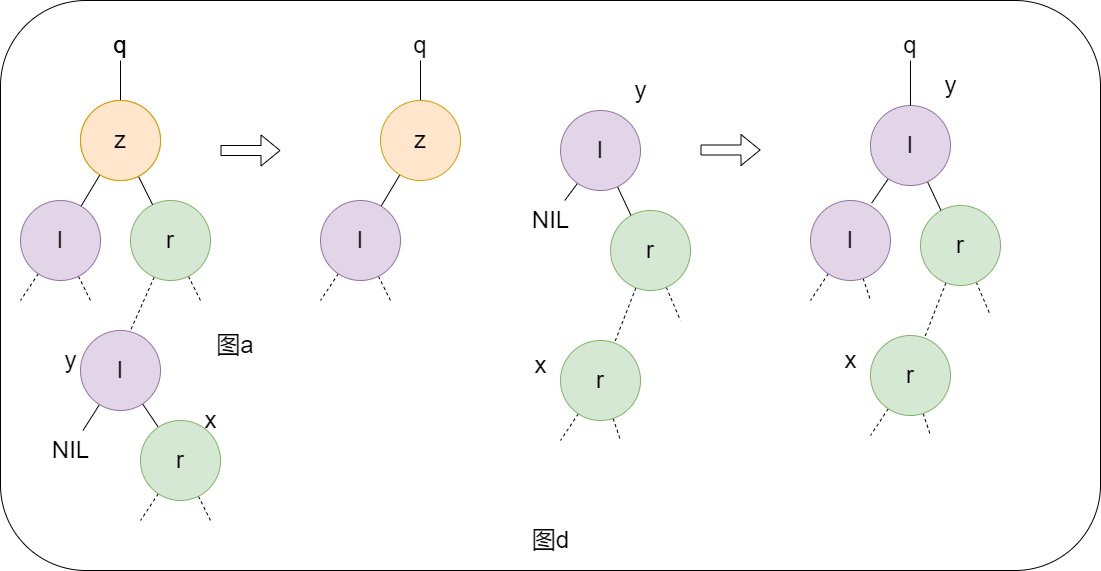
为了方便移动子树，我们可以先定义一个子过程trans_plant，代表用另一颗子树v替换一颗子树u，并且v成为成为u的双亲：u.p的孩子节点：

trans_plant(T, u, v){
    // u 是树根
    if u.p == NIL then
        T.root = v
    // u 是双亲的左孩子  
    else if u == u.p.left then
        u.p.left = v
    // v 是双亲的右孩子 
	else then
        u.p.righ = v
    if v != NIL then
        v.p = u.p
}

ok,完成这个辅助的过程，我们就可以实现我们的删除操作了：

b_tree_search_delete(T, z){
    // 情况1
    if z.left == NIL then
        trans_plant(T, z, z.right);
    // 情况2
    else if z.right == NIL then
        trans_plant(T, z, z.left);
    else then
        // 由于z的右子树非空，因此右子树的最小关键字节点必然是z的后继
        y = b_tree_search_min(z.right)
        // 如果y不是z的右孩子（情况4），我们先用y的右孩子替换y
        if y.p != z then
            trans_plant(T, y, y.right);
    		y.right = z.right;
    		y.right.p = y;
    	//不管是情况3还是情况4，都要用y替换z
    	b_tree_search_min(T, z, y);
    	y.left = z.left;
    	y.left.p = y;
}

根据指定序列建树

根据给定的序列，我们可以获得一个搜索树，例如，对于序列：

10 8 14 6 9

对应的搜索树为：

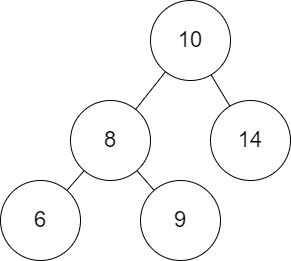
然后，如果给出的树本身就是有序的，例如对于升序数列：

6 8 9 10 14

得到的是一个退化的树，即“树链”：

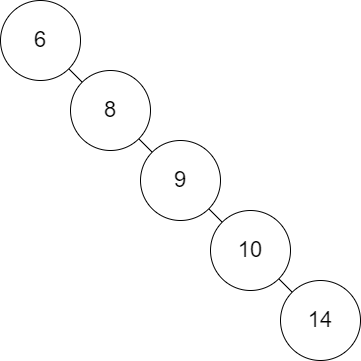
此时，树的搜索时间复杂度不再是$O(\lg n)$，而是$O(n)$，主要是因为在所有的叶子到根的路径中，存在某条路径长度是其他路径的两倍，为了解决这个问题，红黑树被提出。

参考文献

算法导论第三版