CS:APP-Cache Lab

实验包括两个小实验，第一个是仿真Cache，第二个是针对不同情况下，用不同的方式实现矩阵转置。

话不多说，打开电脑，带上键盘，开启实验！

Part-A

第一部分要求我们模拟一个缓存模块，使得其能够计算在给定缓存信息后，面对特定的访存序列，给出最终总的缓存名中、缓存缺失和缓存冲突（替换）的数量。

缓存的信息如下给出：

• s：表明有$2^s$个组
• E：每组有E个缓存行
• b：块的大小是$2^b$个位（好像是字节，不是位，我是按照字节来处理的）

访存序列由文件给出，该文件中由若干行组成，每行由以下形式组成：

[space]operation address,size

operation为以下四者之一：

• I：指令加载（我们不需要处理该类型）

• M：数据修改

• L：数据加载

• S：数据保存

在本实验中，我们只关心operation和address，而且，我们还有以下两个有用的点：

• L或者S最多造成1个”缓存不命中“

• 数据修改M可以视为数据加载，然后存储到同一个地址，因此一个M操作可以造成下面两种情况：

  • ①：两个命中
  • ②：一个不命中和一个名中（可能还有一个替换）

由于我们需要设计一个通用的，即能够处理任意合理的s-E-b组合，因此我们不能够在代码中用数组进行固定缓存组数或者行数，而应该使用链表。

首先，对于缓存，必然是由若干组组成，为了方便，我们要记下缓存总的组数：

typedef struct CacheStruct {
    int groupCnt;
	// 指向第一组    
    GroupItem* groupItemHead;
} Cache;

而对于每一组，同样为了方便，我们要记下该组内有多少行（当然我们也可以在结构体Cache中记录，因为每组内的行数肯定是一样的），我们要记录下该组内用了几行（用于快速判断组内是否已经满了从而进行替换操作），由于我们发生冲突是，使用的是LRU（最近最少使用）策略进行替换，我们还需要记录每行最后一次被访问的时间戳，因此我们可以给每组加一个时钟，因此每个组的结构可以设计成如下：

typedef struct GroupStruct {
    int lineCnt;
    int used;
    int clock;
    // 指向改组内的第一行
    LineItem* lineItemHead;
    // 指向下一组 
    struct GroupStruct* next;
}GroupItem;

而对于每一行，我们要设置一个id，以及有效位，块的大小（也可以在结构体Cache中记录），以及最后一次访问的时间戳：

typedef struct LineItemStruct {
    int id;
    char valid;
    int blockSize;
    int insertClock;
    // 指向下一行
    struct LineItemStruct* next;
} LineItem;

设计好这些数据后，完整的代码就呼之欲出了，由于代码比较冗长，大家可以到【GitHub】上参考

值得注意的是，处理L和S的逻辑是一样的，因为都是要先判断缓存中存不存在，不存在则加载进来，最后不管怎么样，都会更新时钟，因此可以把这两个处理函数合二为一，但是为了体现模块化思想，我还是保留了。

测试：

make
./test-csim
                        Your simulator     Reference simulator
Points (s,E,b)    Hits  Misses  Evicts    Hits  Misses  Evicts
     3 (1,1,1)       9       8       6       9       8       6  traces/yi2.trace
     3 (4,2,4)       4       5       2       4       5       2  traces/yi.trace
     3 (2,1,4)       2       3       1       2       3       1  traces/dave.trace
     3 (2,1,3)     167      71      67     167      71      67  traces/trans.trace
     3 (2,2,3)     201      37      29     201      37      29  traces/trans.trace
     3 (2,4,3)     212      26      10     212      26      10  traces/trans.trace
     3 (5,1,5)     231       7       0     231       7       0  traces/trans.trace
     6 (5,1,5)  265189   21775   21743  265189   21775   21743  traces/long.trace
    27

TEST_CSIM_RESULTS=27

Part-B

上面的实验是开胃菜，只要有一些程序设计思想的应该都能做出来，该部分的实验才是需要花点时间的。

我们先来一个最简单的，将transpose_submit改为下面的逻辑：

void transpose_submit(int M, int N, int A[N][M], int B[M][N]) {
	int i, j, tmp;

    	for (i = 0; i < N; i++) {
        for (j = 0; j < M; j++) {
            tmp = A[i][j];
            B[j][i] = tmp;
        }
    } 
}

同时只注册我们的函数：

void registerFunctions()
{
    /* Register your solution function */
    registerTransFunction(transpose_submit, transpose_submit_desc); 

    /* Register any additional transpose functions */
//    registerTransFunction(trans, trans_desc); 

}

测试：

make
./test-trans -M 32 -N 32
Function 0 (1 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 0 (Transpose submission): hits:869, misses:1184, evictions:1152

Summary for official submission (func 0): correctness=1 misses=1184

TEST_TRANS_RESULTS=1:1184

我们可以看到，没有任何优化的情况下，缓存缺失有1184次，离目标<300还很远。

我们再来看看访存情况：

./csim-ref -v -s 5 -E 1 -b 5 -t trace.f0 > debug.txt
cat debug.txt
S 10c080,1 miss 
L 18c0c0,8 miss 
L 18c0a4,4 miss 
L 18c0a0,4 hit 
L 10c0a0,4 miss eviction 
S 14c0a0,4 miss eviction 
L 10c0a4,4 miss eviction 
S 14c120,4 miss 
L 10c0a8,4 hit 
S 14c1a0,4 miss 
L 10c0ac,4 hit 
S 14c220,4 miss 
L 10c0b0,4 hit 
S 14c2a0,4 miss 
L 10c0b4,4 hit 
S 14c320,4 miss 
....

从结果来看，我们知道了两个数组之间的地址差为0x14c0a0-0x10c0a0=0x40000.

此外，我们还知道s=5,E=1,b=5,即一共32组，每组一行，每块2^5=32字节,即一个块可以放8个int类型数据。

对于一个32位地址，会按照下面的格式进行解析：

------------------------------------------------------
|  id(22-bit) | groupId(5-bit) | block-offset(5-bit) |
------------------------------------------------------

意味着代码中的A数组起始地址和B数组起始地址都会被映射到同一组，准确来说，对于地址&A[i][j]和&B[i][j]都会被映射到同一组，但是对应的id不同。数组A和数组B元素对应的组号大致如下：

A || B:
0...0 1...1 2..2 3...3
4...4 ................
8...8 ................
12...12 ................
16...16 ................
20...20 ................
24...44 ................
28...28 ................

即groupID_A[0][0]=groupID_B[0][0]=0，groupID_A[1][0]=groupID_B[1][0]=4

因此我们应该尽量避免访问完数组A后立马访问数组B，避免将刚刚加载进缓存的数据因为冲突而被替换出去，由于每行可以放8个元素，因此如果我们可以保障连续读取的8个数字在同一组是最好的情况，因此我们可以将数组分块遍历。此外，我们的局部变量个数比较少的时候，会使用寄存器保存他们，引用它们不会对缓存造成影响，因此我们要善于利用局部变量。

32*32

我们可以分块成8*8的矩阵，一开始的时候，我们可以一次性读取A数组的8个数字（A[0][0]~A[0][7]），因为这8个数字都是在同一行，读取完后缓存情况如下，绿色代表在缓存中，每个数字代表该元素对应的组号

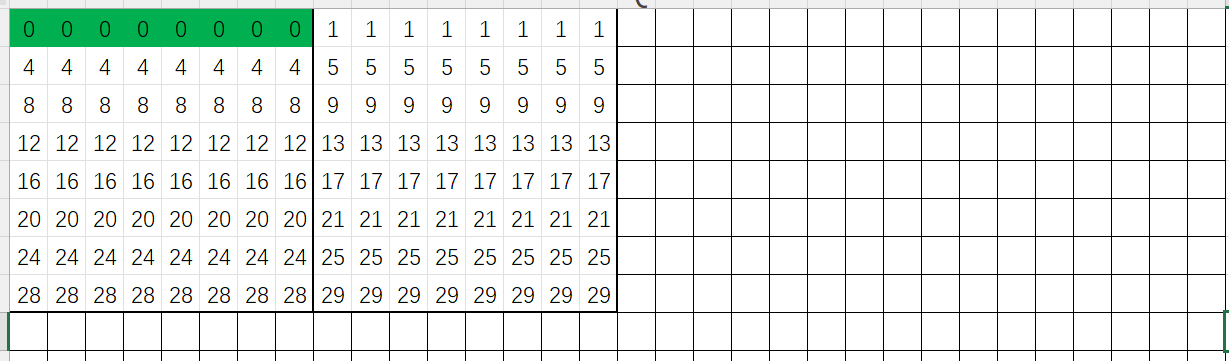
下一步就是进行转置操作，由于数组B和数组A对应位置的元素将会映射到同一组，因此缓存中会先进行替换，再逐一加载进缓存，第一次转置完毕后， 缓存中都是数组B的元素：

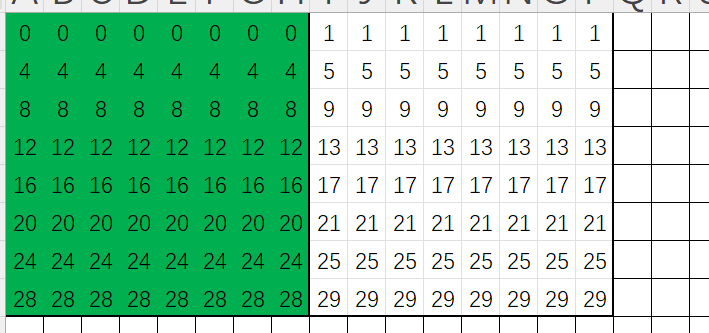
下图表示转置情况，黄色代表转置完毕：

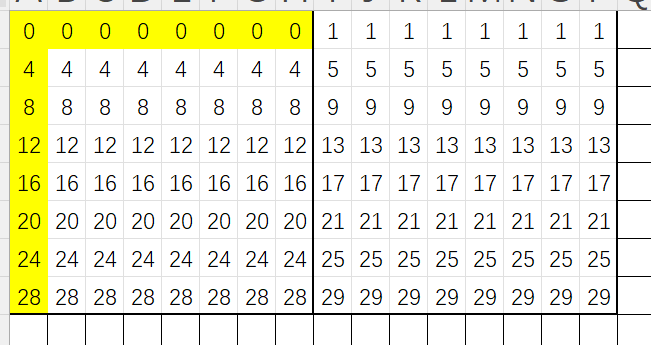
接下来是重点了，由于我们缓存中有大量的数组B的数据，我们应该利用这点，我们先读取A[1][1]~A[1][7]共7个数字，此时会发生一次缓存替换，先不管，然后将这些数据进行转置，转置过程只会在保存B[1][1]时候发生缓存替换，后面B[2][1]~B[7][1]都缓存命中，转置后的情况为：

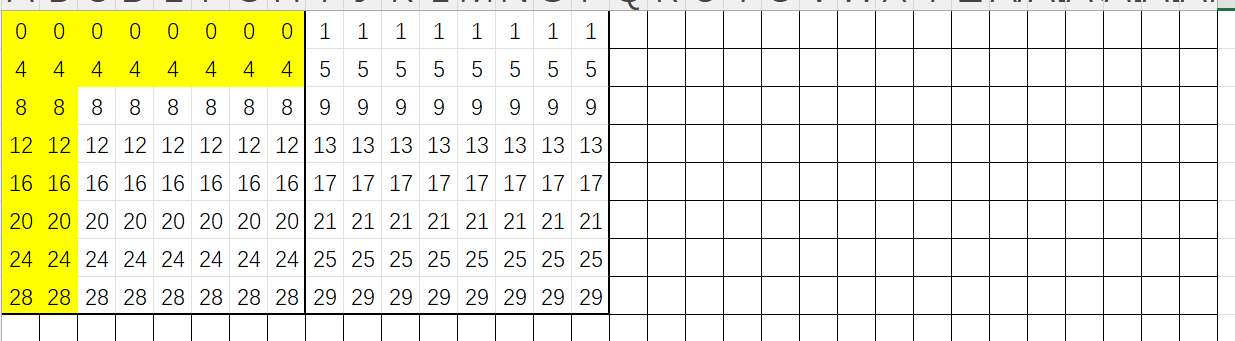
按照这个思路，继续完成这个小矩阵剩余部分，再转到下一个小矩阵即可，代码如下：

void transpose_submit(int M, int N, int A[N][M], int B[M][N]) {
    if (M == 32) {
        int tmp1, tmp2, tmp3, tmp4, tmp5, tmp6, tmp7, tmp8;
        for (int bi = 0; bi < 4; bi++) {
            for (int bj = 0; bj < 4; bj++) {
                // 上面是迭代分块矩阵的逻辑（32 / 8 = 4）
                // 下面是小矩阵内从按行进行
                for (int k = 0; k < 8; k++) {
                    tmp1 = A[bi * 8 + k][bj * 8];
                    tmp2 = A[bi * 8 + k][bj * 8 + 1];
                    tmp3 = A[bi * 8 + k][bj * 8 + 2];
                    tmp4 = A[bi * 8 + k][bj * 8 + 3];
                    tmp5 = A[bi * 8 + k][bj * 8 + 4];
                    tmp6 = A[bi * 8 + k][bj * 8 + 5];
                    tmp7 = A[bi * 8 + k][bj * 8 + 6];
                    tmp8 = A[bi * 8 + k][bj * 8 + 7];

                    B[bj * 8][bi * 8 + k] = tmp1;
                    B[bj * 8 + 1][bi * 8 + k] = tmp2;
                    B[bj * 8 + 2][bi * 8 + k] = tmp3;
                    B[bj * 8 + 3][bi * 8 + k] = tmp4;
                    B[bj * 8 + 4][bi * 8 + k] = tmp5;
                    B[bj * 8 + 5][bi * 8 + k] = tmp6;
                    B[bj * 8 + 6][bi * 8 + k] = tmp7;
                    B[bj * 8 + 7][bi * 8 + k] = tmp8;
                }
            }
        }
    }
}

测试：

make
 ./test-trans -M 32 -N 32
 Function 0 (1 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 0 (Transpose submission): hits:1765, misses:288, evictions:256

Summary for official submission (func 0): correctness=1 misses=288

TEST_TRANS_RESULTS=1:288

低于300，满足测试要求。

64*64

如果我们仍然以分块的方式进行，由于前4行和后4行都映射到同一组，我们只能以4*4的分块方式：

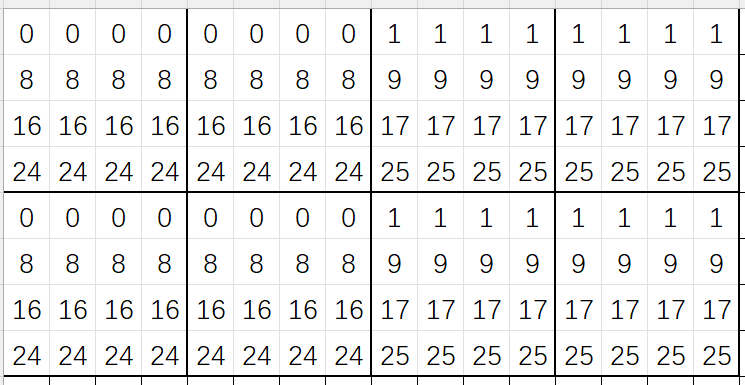
但是很遗憾，按照4*4的逻辑，我们只能拿一点分：

./test-trans -M 64 -N 64
Function 0 (1 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 0 (Transpose submission): hits:6497, misses:1700, evictions:1668

Summary for official submission (func 0): correctness=1 misses=1700

TEST_TRANS_RESULTS=1:1700

距离1300还有一定差距。

进一步优化的代码我实在想不出了，参考了【别人的做法】：

仍然是考虑8*8，但是在8*8中，又继续分4*4，处理过程如下：

• 第一步，利用局部变量将A的左上和右上一次性复制给B，处理完成后，缓存中是B的左上和右上部分
• 第二步，用本地变量把B的右上角存储下来，此时缓存名中
• 第三步，将A的左下复制给B的右上
• 第四步，利用上述存储B的右上角的本地变量，把A的右上复制给B的左下
• 第五步，把A的右下复制给B的右下

由于这部分不是我写的，代码就参照【GitHub】即可

测试：

make
 ./test-trans -M 64 -N 64
 
Function 0 (1 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 0 (Transpose submission): hits:9017, misses:1228, evictions:1196

Summary for official submission (func 0): correctness=1 misses=1228

TEST_TRANS_RESULTS=1:1228

低于1300，达到要求！

61*67

由于不是方阵，因此想要愉快地进行优化，没啥路子，而且数组A和数组B对应位置不一定会映射到同一组，真要优化起来，估计很复杂，试一下暴力破解！从8*8开始，到16*16，最后发现16*16的方式可以通过：

    else {
        for (int i = 0; i < N; i += 16)
            for (int j = 0; j < M; j += 16)
                // 要注意不能超出边界N 下面的循环同理
                for (int k = i; k < i + 16 && k < N; k++)
                    for (int l = j; l < j + 16 && l < M; l++)
                        B[l][k] = A[k][l];
    }

测试：

make
./test-trans -M 61 -N 67

Function 0 (1 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 0 (Transpose submission): hits:6186, misses:1993, evictions:1961

Summary for official submission (func 0): correctness=1 misses=1993

TEST_TRANS_RESULTS=1:1993

低于2000，满足条件！

总结

遍历数组时候，尽量以行的方式进行，因为我们可以最大化利用缓存。

---