黄阿信的个人博客

问题抽象建模

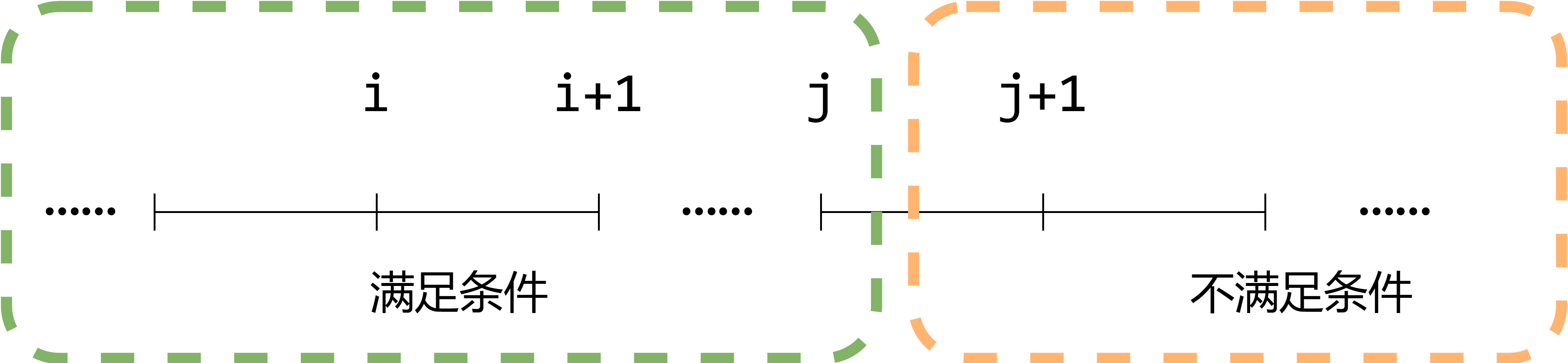
本文所说的二分算法，和二分查找算法有些区别，即在给定的一个区间，左边若干连续长度内是满足一定条件的，右边若干连续长度内都是不满足该条件的，我们要求出这个分界点。

通过暴力法，我们可以直接简单地从区间的最小值进行迭代，该时间复杂度为$O(n*T)$，n是区间长度，$T$是判断指定数字是否满足条件的花销。

然而，如果区间非常大，那么上述过程可能会变得非常慢。

实际上，由于区间左部分是相同性质的，右边也是具有另一个性质，我们可以使用二分法，即每次使用区间的中间值去判断，如果中间值表现出和左边一致，则这个分界点一定在中间值的右边，即我们把要检查的区间长度将为原来的**一半。**这个过程时间复杂度可以降为$O(log(n)*T)$

2fenp1

bool check(check_num):
	// 根据一定逻辑，判断 check_num 是在左区间还是右区间
	
	
// 二分算法
int bin(){
	left, right = MIN,MAX
	while 区间可分 do:
		mid = (left + right) / 2
		if check(mid) 更新左区间边界（或右区间边界）
		else 更新右区间边界（或左区间边界）
	
	return left 或者 right	
}

实际上，二分查找通常有三种细节略有不同的实现方式：左闭右闭、左闭右开和左开右闭，下面结合基本例子，分别讲述这三种情况下的实现方式。

阿珍和阿强是一对情侣，他们在玩一个游戏，阿珍先在心里默念一个数字target，范围是1到2147483647，然后要阿强猜出这个数字是多少，每次阿强猜一个数字num的时候，阿珍只会回答num“小于等于”或者"大于"target，但是我们知道每个人的耐心是有限的，阿强能够在40次之间将这个数字猜中，从而他们今晚能够出去看月亮吗？

左闭右闭

我们先将该问题抽象成之前的问题，即对于在[1,target]中的数字都是满足“小于等于target”条件的，[target+1,INF]中的数字都是不满足“小于等于target”条件的，而满足该条件的最大值，就是我们的目标值。

关于二分求解，大致的程序如下：

bool check(int check_num){
    if(check_num <= TARGET)return true;
    else return false;
}
int bin(){
    int left, right = MIN,MAX
	while (left < right){
        int mid = (left + right + 1) / 2;
        if (check(mid)){
            left = mid;
        }else{
            right = mid - 1;
        }
    }
	return left;
}

由于我们定义target 是在一个在左闭右闭的区间里，也就是 [left, right]。那么就要满足：

区间可分逻辑：while(left < right)
更新区间边界逻辑：如果check(mid)返回值是真，则[left,mid]中的所有元素也一定能够满足“小于等于target”条件，但是满足条件的最大值应该在[mid,right]中，不可能在[left,mid-1]中，因此left = mid；反之，如果其返回值是假，则说明满足条件的最大值不可能在[mid,right]中，因此right = mid - 1；
关于mid的计算方式：mid作用是不断减小区间长度，当区间长度不小的时候，向上取整和向下取整都是无关紧要的，我们只需要关注当区间只有两个元素时候，该如何计算mid？我们使用逆推的思想，由于我们更新区间的方式中，存在left = mid，假设我们是向下取整，left=2,right=3，那么mid是2，即mid=left，而left是一定满足check函数的条件，即将出现死循环！因此我们应该是向上取整。

假如我们要转换为满足条件的最小值，如何求解？即我们将条件转为“大于等于target”，实际上，也只需要将相应程序改为：

bool check(int check_num){
    if(check_num >= TARGET)return true;
    else return false;
}
int bin(){
    int left = MIN, right = MAX;
	while (left < right){
        int mid = (left + right ) / 2;
        if (check(mid)){
            right = mid;
        }else{
            left = mid + 1;
        }
    }
	return right;
}

区间可分逻辑：while(left < right)
更新区间边界逻辑：如果check(mid)返回值是真，则[mid,right]中的所有元素也一定能够满足“大于等于target”条件，但是满足条件的最小值应该在[left,mid]中，不可能在[mid + 1,right]中，因此right = mid；反之，如果其返回值是假，则说明满足条件的最大值不可能在[left,mid]中，因此left= mid + 1；
关于mid的计算方式：我们使用逆推的思想，由于我们更新区间的方式中，存在right = mid，假设我们是向下取整，left=2,right=3，那么mid是2，即mid=left，而right是一定满足check函数的条件，即将出现死循环！因此我们应该是向上取整。

简单来说，更新区间时候，如果是left=mid，则向上取整，否则向下取整。

左闭右开

此时，我们的target定义在左闭右开，即[left,right)中，还是先以满足条件的最大值为例，测试条件为“小于等于target”，即[left,right-1]中的元素都满足条件，但是right不满足！明白这点很重要！

bool check(int check_num){
    if(check_num <= TARGET)return true;
    else return false;
}
int bin(){
    int left = MIN, right = MAX;
	while (left + 1 < right){
        int mid = (left + right) / 2;
        if (check(mid)){
            left = mid;
        }else{
            right = mid;
        }
    }
	return left;
}

区间可分逻辑：while(left + 1< right)，为什么呢？因为我们的区间是开区间，左边边界永远不会等于右边边界，最小差值为1.
更新区间边界逻辑：如果check(mid)返回值是真，则[left,mid]中的所有元素也一定能够满足“小于等于target”条件，但是满足条件的最大值应该在[mid,right]中，不可能在[left,mid-1]中，因此left = mid；反之，如果其返回值是假，则说明满足条件的最大值不可能在[mid,right]中，因此right = mid ；注意，我们新的区间仍然要满足开区间的定义！即右边节点不满足条件
关于mid的计算方式：由于是使用左闭右开的思想，即一旦满足left + 1 == right条件，此时就会跳出循环，因此向上取整和向下取整，都无关紧要了。

左开右闭

假如我们要转换为满足条件的最小值，即我们将条件转为“大于等于target”，即[left+1,right]中的元素都满足条件，但是left不满足，则更新代码如下：

using namespace std;
 int TARGET = 1024;
const int MIN = 1, MAX = 999999;
bool check(int check_num){
    if(check_num >= TARGET)return true;
    else return false;
}
int bin(){
    int left = MIN, right = MAX;
	while (left + 1 < right){
        int mid = (left + right) / 2;
        if (check(mid)){
            right = mid;
        }else{
            left = mid;
        }
    }
	return right;
}

更新区间边界逻辑：如果check(mid)返回值是真，则[mid,right]中的所有元素也一定能够满足“大于等于target”条件，但是满足条件的最小值应该在[left,mid]中，不可能在[mid + 1,right]中，因此right = mid；反之，如果其返回值是假，则说明满足条件的最大值不可能在[left,mid]中，因此left= mid；注意，我们新的区间仍然要满足开区间的定义！即左边节点不满足条件

总结

二分法是个很好用的工具，但是依据不同情况，可以有不同的实现方法，相比之下，左闭右闭的方法通用性比较大。

关于二分算法中的边界问题的思考

问题抽象建模

左闭右闭

左闭右开

左开右闭

总结