黄阿信的个人博客

忙里偷闲，记录一下使用分治法求逆序数的实现过程。

算法设计

**逆序：**在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。例如<3,1>就是一个逆序。

**逆序数：**给定数列中，逆序的数目。例如数列:

[1,3,4,2]

逆序数是2.

暴力法

很容易就想到的一个方法就是从头开始扫描，然后对于每一个扫描到的数字a，考察后面的每一个数字b，观察其是否满足逆序的定义，例如对于上述数列，对于数字1，逆序数为0；对于数字3，逆序数为1（<3,2>），依此类推，最终数列总的逆序数为2.

很遗憾，该算法复杂度为$O(n^2)$,对于暴躁的张三来说，当其要计算长度为10000的数列的逆序数时候，他是无法接受长时间等待的，~~因为他还要去和阿珍约会呢~~

分治法

分而治之，逐个击破

分治法的思想是将原问题分解成若干个子问题，而所有的子问题进行简单处理后就可以得到原问题的解。求解子问题的过程亦可以继续分解成子子问题，而子问题分解到“原子问题”（原子问题好像也不太严谨，大概意思就是一个可以直接求解的问题）后可以立即得到解。

例如对于下面的数列：我们可以每次把子数列分成两半，分别求左半部分和右半部分的逆序数

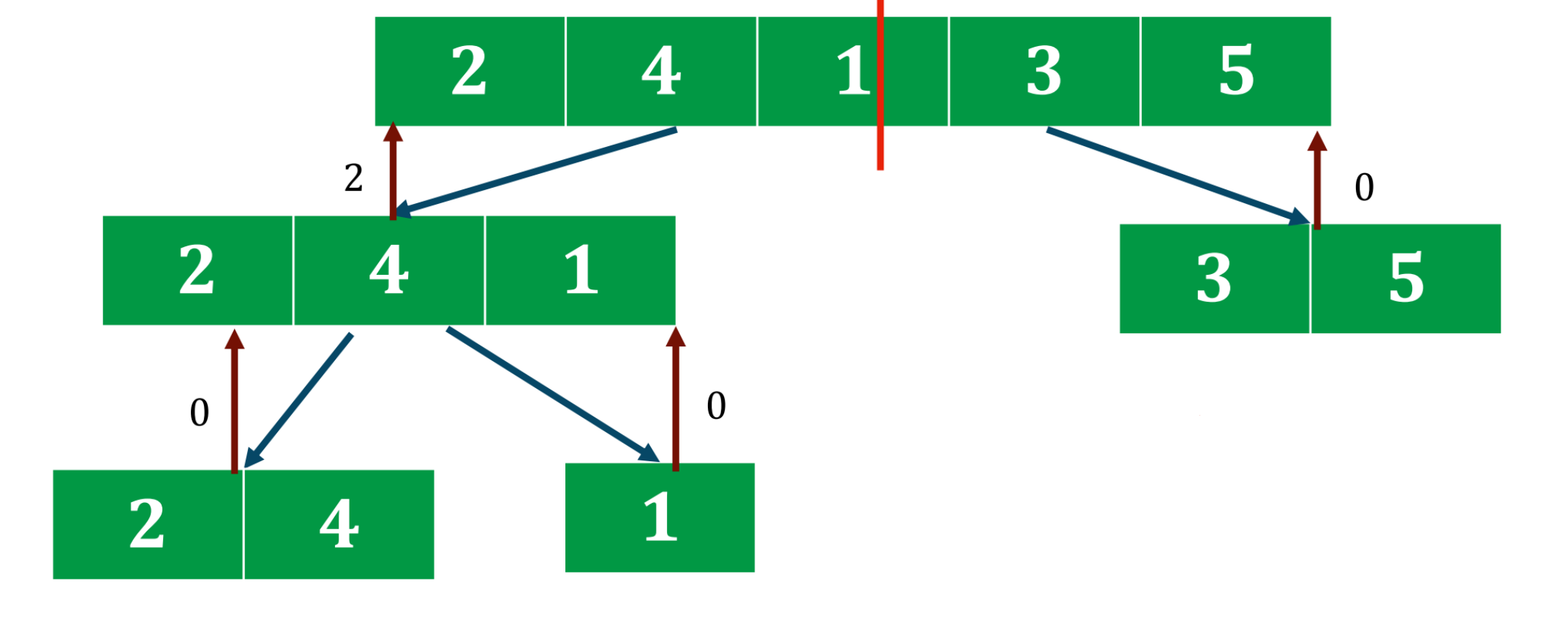
那我们如何还原出原问题的解呢？即未分解问题时候的逆序数。仔细想想，我们已经计算出了左右两边逆序数leftCnt、rightCnt，那么我们再计算出在“ 一个数字取自左边，另一个数字取自右边”的情况下，逆序数cnt的大小，原问题不就是这三个数字之和吗？

关键是怎么求cnt?

老方法？依次从左边选一个数字a，再依次从右边选一个数字b，很抱歉，这样子下来要判断$\frac{n}{2}*\frac{n}{2}=\frac{n^2}{4} $次，综合下来时间复杂度还是$O(n^2)$。

仔细想想，我们要判断的数字一个来自左边，一个来自右边，如果我们分别让左边和右边有序，然后分别从第一个开始遍历，根据遍历到的数字进行计算逆序数，根据有序的性质，遍历完后逆序数也求解出来了，整个过程中，排序花费$O(n\log n)$，遍历花费$O(n)$，即合并子问题花费$O(n\log n)$.

关于合并过程的仔细分析，如下(简单起见，数列中不包含相同元素)：

先将左右两部分排序，设置两个指针，分别从左右两部分进行遍历，设左边遍历得到的数字是a[i]，右边的是b[j]。

右边的指针j不断往后移动（尚未到结尾，如果到结尾，则到步骤3），直到b[j]恰好是右半部分中第一个不小于a[i]的数字，即在右半部分中b[j]的左边都是小于a[i]的，此时，由a[i]作为第一个数字组成的跨越左右两部分的数对（或者说序偶）中，逆序数刚好就是右半部分中b[j]的左边的数字个数。说起来有点绕口，看看下面的图：

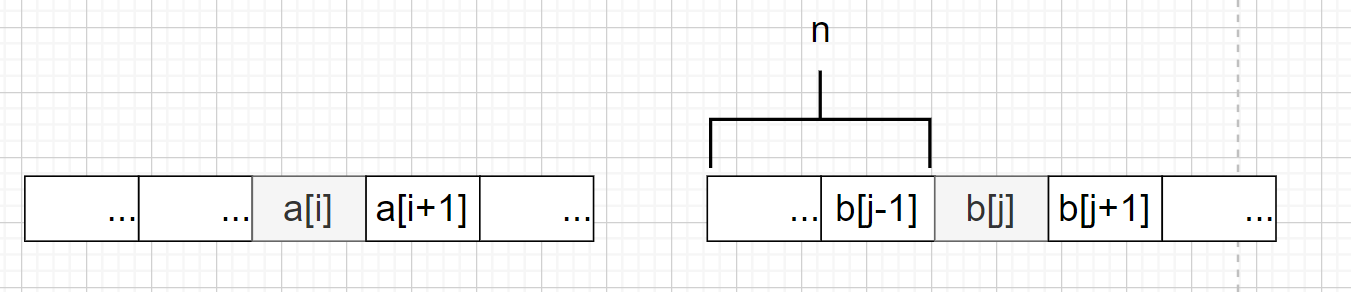
此时逆序数cnt要加上n.

左边的指针要往后移动，即指向a[i+1],那么就会有两种情况：

①a[i+1]>b[j]:这个很好解决，继续回到步骤1即可。
②a[i+1]<b[j]:由于b[j]的左边都是小于a[i]，即存在这样的关系：b[j]>a[i+1]>a[i]>b[j-1]，故此时由a[i+1]作为第一个数字组成的跨越左右两部分的数对（或者说序偶）中，逆序数也是n，此时逆序数cnt要加上n.下一步左边的指针要往后移动，继续步骤②，直到左边的指针指向元素比右边指针指向的大，回到步骤1，假若左边的指针先到了左半部分的最右边，则到步骤3。

此时要么左半部分先遍历完，要么右半部分先遍历完，假如是左边先遍历完，则说明此时“跨越左右两半部分的逆序数”统计完成，即cnt是正确的值，跳步骤4.如果是右半部分先遍历完成，则说明左边尚未遍历完成的数字都要比右半部分的数字大，根据这个条件计算逆序数后，转步骤4.
将leftCnt + rightCnt + cnt作为原问题的解。

算法分析

下面进行时间复杂度分析，我们子问题个数是2（分别递归求解左右两个部分），每个子问题的规模是原来的一半，合并子问题花费$O(n\log n)$。

则： $$ T(n)=2T(\frac{n}{2} )+O(n \log n) $$ 根据主定理，得 $$ T(n)=O(n \log n) $$

算法实现

#include<iostream>
#include<algorithm>
using namespace std;
const int LEN = 100000 + 2;
int list[LEN], length;
long long reverseOrderNumber(int left, int right){
    if (left >= right)return 0;
    if (left + 1 == right)return list[left] > list[right];
    int mid = (left + right) >> 1;
    // 分别求解子问题
    long long leftCnt  = reverseOrderNumber(left, mid);
    long long rightCnt = reverseOrderNumber(mid + 1, right);
    // 排序左右两半部分
    int *l1 = list + left, *r1 = list + mid - left + 1 + left;
    sort(l1, r1);
    sort(r1, list + right + 1);
    // 计算跨左右部分的逆序数
    int i = left, j = mid + 1;
    long long cnt = 0;
    while(i <= mid && j <= right){
        // 在右边寻找第一个大于 a[i] 的元素
        while(j <= right && list[i] > list[j])j++;
        if (j > right)break;
        while(i <= mid && list[i] < list[j]){
            i++;
            cnt += j - 1 - mid;
        }
    }
    // 左边尚未遍历完的数字都要比右半部分的大
    if(j > right) cnt += (mid - i + 1) * (right - mid);
    // 合并子问题
    return leftCnt + rightCnt + cnt;
}
int main(){
    // printf("input the length:\n");
    scanf("%d", &length);
    // printf("input the value:\n");
    for (int i = 0; i < length;i++)
        scanf("%d", &list[i]);
    printf("%lld\n", reverseOrderNumber(0, length - 1));
    return 0;
}
/*

4
5 3 7 2

4
5 9 7 2

8
5 9 12 16 2 3 13 14

3
7 4 3

6
2 6 3 4 5 1

*/

实际上排序过程也可以使用归并排序，并且排序过程就可以计算逆序数了，不过归并排序过程要辅助空间，这里就没有采用。

基于分治法的特定数列逆序数求法

算法设计

暴力法

分治法

算法分析

算法实现